Fragment A P.R. n° 2 / 2 – Papier original : RO 321 r°/v° et 325 r°/v°
Copies manuscrites du XVIIe s. : C1 : APR n° 207 à 215 p. 71 à 75 / C2 : p. 97 à 102
Éditions de Port-Royal :
Chap. III - Veritable Religion prouvée par les contrarietez : 1669 et janv. 1670 p. 33-34, 39-40 / 1678 n° 1 p. 36-37, n° 10 à 12 p. 42
Chap. IV - Il n’est pas incroyable que Dieu s’unisse à nous : 1669 et janv. 1670 p. 45 à 47 / 1678 n° 1 p. 48-49
Chap. XXVIII - Pensées chrestiennes : 1669 et janv. 1670 p. 272 / 1678 n° 76 p. 265
Chap. XVIII - Dessein de Dieu de se cacher aux uns, et de se découvrir aux autres : 1669 et janv. 1670 p. 136-137 / 1678 n° 1 p. 135-136
Éditions savantes : Faugère II, 147, XVI / Havet XII.2 à 5 ; XII.20 ; XX.1 / Brunschvicg 430 / Tourneur p. 221 / Le Guern 139 / Lafuma 149 / Sellier 182
______________________________________________________________________________________
Exemples d’espaces infinis égaux au fini.
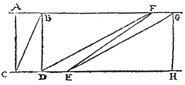
L’exemple le plus élémentaire se trouve dans La Vérité des sciences du P. Mersenne, La Vérité des sciences, IV, XII, p. 876 sq. Si, dans un rectangle ABDC, construit entre les parallèles AE et CH, on fait glisser la largeur AB sur AF, par exemple jusqu’en FG, le parallélogramme CFGD est égal au rectangle. Mais « imaginez-vous maintenant que ces parallèles soient prolongées du pôle arctique à l’antarctique, ou cent mille fois plus loin, et que le parallélogramme DG aille depuis le commencement des parallèles jusques à la fin, je dis qu’il ne contiendra pas davantage que le parallélogramme AD ». Si l’on renvoie FG à l’infini sur AE, le parallélogramme lui-même s’étendra à l’infini, alors que sa surface demeurera constante. Imaginons que ces parallèles soient prolongées à l’infini, le nouveau parallélogramme, qui sera infiniment fin, ne contiendra pourtant « pas davantage que le parallélogramme AD, par où quelques Théologiens concluent qu’un ange peut être présent au ciel, et en la terre pourvu qu’il puisse se rendre à présent l’espace d’un pouce, ou à un plus petit espace mille fois, supposé aussi qu’il puisse donner telle figure qu’il voudra à la sphère de son activité » (En marge : Comment chaque ange peut être présent au ciel et en la terre.)
Arnauld Antoine et Nicole Pierre, La Logique ou l’art de penser, IV, 1, éd. D. Descotes, Paris, Champion, 2011, p. 519-520, proposent un exemple plus sérieux : si l’on divise un carré par la moitié, puis l’une des moitiés par la moitié, et ainsi de suite, en rangeant ces moitiés successives côte à côte, on engendre une surface en escalier qui se prolongera toujours, puisque la division par moitiés ne s’achève jamais. Cependant la somme des portions est égale à la totalité du rectangle original.
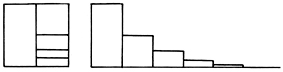
Arnauld Antoine et Nicole Pierre, La logique ou l’art de penser, IV, 1, éd. de 1664, éd. D. Descotes, Paris, Champion, 2011, p. 514-520.
« Mais il faut remarquer qu’il y a des choses qui sont incompréhensibles dans leur manière, et qui sont certaines dans leur existence ; on ne peut concevoir comment elles peuvent être, et il est certain néanmoins qu’elles sont [...].C’est par cette diminution infinie de l’étendue qui naît de sa divisibilité, qu’on peut prouver ces problèmes qui semblent impossibles dans les termes : trouver un espace infini égal à un espace fini, ou qui ne soit que la moitié, le tiers, etc. d’un espace fini. On les peut résoudre en diverses manières, et en voici une assez grossière, mais très facile. Si l’on prend la moitié d’un carré, et la moitié de cette moitié, et ainsi à l’infini, et que l’on joigne toutes ces moitiés par leur plus longue ligne, on en fera un espace d’une figure irrégulière, et qui diminuera toujours à l’infini par un des bouts, mais qui sera égal à tout le carré ; car la moitié, et la moitié de la moitié, plus la moitié de cette seconde moitié, et ainsi à l’infini, font le tout ; le tiers et le tiers du tiers, et le tiers du nouveau tiers, et ainsi à l’infini font la moitié. Les quarts pris de la même sorte font le tiers, et les cinquièmes le quart. Joignant bout à bout ces tiers ou ces quarts, on en fera une figure qui contiendra la moitié ou le tiers de l’aire du total, et qui sera infinie d’un côté en longueur, en diminuant proportionnellement en largeur.
L’utilité que l’on peut tirer de ces spéculations n’est pas simplement d’acquérir ces connaissances, qui sont d’elles-mêmes assez stériles ; mais c’est d’apprendre à connaître les bornes de notre esprit, et à lui faire avouer malgré qu’il en ait, qu’il y a des choses qui sont, quoiqu’il ne soit pas capable de les comprendre ; et c’est pourquoi il est bon de le fatiguer à ces subtilités, afin de dompter sa présomption, et lui ôter la hardiesse d’opposer jamais ses faibles lumières aux vérités que l’Église lui propose, sous prétexte qu’il ne les peut pas comprendre ; car puisque toute la vigueur de l’esprit des hommes est contrainte de succomber au plus petit atome de la matière, et d’avouer qu’il voit clairement qu’il est infiniment divisible, sans pouvoir comprendre comment cela se peut faire, n’est-ce pas pécher visiblement contre la raison, que de refuser de croire les effets merveilleux de la toute-puissance de Dieu, qui est d’elle-même incompréhensible, par cette raison que notre esprit ne les peut comprendre ? »
Il existe des exemples plus complexes.
Dans un appendice du De dimensione parabolae, Torricelli y définit de la manière suivante le solide hyperbolique aigu : si une hyperbole d’asymptotes AB et AC tourne autour de la droite fixe AB, elle engendre un solidum hyperbolicum acutum dont la hauteur s’étend à l’infini vers A, puisque l’hyperbole ne rejoint jamais ses asymptotes, sinon à l’infini.
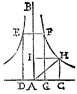

La thèse de Torricelli est que ce solide, tout infini qu’il soit du côté de A, est de volume fini, et égal à celui d’un cylindre connu : le solide élevé sur la base EF est égal au cylindre dont la hauteur est ED et le diamètre de la base EF ou DG.
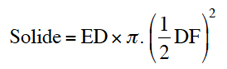
L’énoncé est le suivant : « solidum acutum hyperbolicum infinite longum, sectum plano ad axem recto, una cum cylindro suae basis, aequale est cylindro cuidam recto, cujus basis sit latus versum, sive axis hyperbolae, altitudo vero sit aequalis semidiametro basis ipsius acuti solidi » (De dimensione parabolae, Opera geometrica, p. 115 ; Torricelli, Opere, I, Faenza, 1919, p. 193.).Torricelli en donne deux démonstrations différentes, l’une par la méthode des indivisibles inspirée de Cavalieri, l’autre conforme à la technique classique des anciens par inscriptions et circonscriptions. Roberval donne une autre démonstration de la même proposition.
Voir Mersenne Marin, Universae geometriae mixtaeque mathematicae synopsis de 1644, Praef. 2 ; et Correspondance, XII, p. 266.
Itard Jean, “La lettre de Torricelli à Roberval d’octobre 1643”, in Revue d’histoire des sciences, 1975, XXVIII-2, p. 113-124.
Mancosu Paolo, Philosophy of mathematics and mathematical practice in the seventeenth century, New York- Oxford, Oxford University Press, 1996, p. 132.
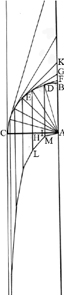
Roberval donne un exemple à deux dimensions avec les courbes quadratrices, auxquelles il pensait attacher son nom. Soit un triligne rectangle ABC, dont la ligne courbe convexe BC est extérieure à la droite BC. Sur l’arc BC on prend un nombre quelconque de points D, E, et on trace les tangentes qui coupent l’axe AB prolongé vers K en F, G. On abaisse des points D, E, les perpendiculaires à AC, soit EH et DI. Puis à partir de A on mène AM parallèle à DF, AL parallèle à EG, AN parallèle à CK. En prolongeant RC, EH, DI, on obtient les points M, L, N, qui forment la quadratrice AMLN. Dans la plupart des cas, la ligne AMLN coupe la droite RCN qui passe par C, extrémité du triligne. La figure AMLN est alors close et finie. Mais si le triligne est un quart de cercle par exemple, la tangente CN à la courbe est parallèle à l’axe AB, et CR ne coupe AK qu’à distance infinie. Or par la construction précédente la verticale tirée de la courbe est égale à la distance du point A à l’intersection de AK avec la tangente : comme DF et AM sont parallèles, DM égale AF ; pour une raison analogue, EL égale AG. Mais si, comme sur la figure ci-dessous, la tangente CR est parallèle à AB, si K est renvoyé à l’infini, CN aussi sera infini. La quadratrice AMLN coupant CN à l’infini, la surface qu’elle délimite se prolonge indéfiniment en longueur. Torricelli envoya à Roberval sa propre démonstration. |
|
Roberval démontre pourtant que cet espace a, comme le solide hyperbolique, une dimension finie.
De nouveau, il part du fini, considérant la quadratrice ABCN dans le cas où la courbe n’est pas tangente à CR. Il forme le parallélogramme AFDM, double du triangle ADF. Puis du parallélogramme EGAL, il retranche la portion déterminée par DM, pour ne considérer que le parallélogramme partiel ED’M’L, double du triangle correspondant ED’A, car ED’ et AL étant parallèles, le triangle et le parallélogramme ont même base ED’ et égale hauteur. Pour tous les autres triangles et parallélogrammes, le même rapport de 1 à 2 subsiste. Cependant, plus on les multiplie, plus l’ensemble des triangles tend à se confondre avec le triligne ABC, et plus la somme des parallélogrammes se rapproche du quadriligne ABCN. Par conséquent quand les divisions de la courbe sont très nombreuses
ABCN = 2 ABC
ACN = ABC
Soit à présent la surface limitée par AMLN prolongée à l’infini le long de CN. Tous les parallélogrammes à l’infini n’en demeurent pas moins doubles de tous les triangles correspondants : la même relation demeure donc entre le triligne fini et le surface infinie en longueur.
Voir les indications et les textes relatifs à ces disputes entre Roberval et Torricelli dans Lettre de Torricelli au P. Niceron de mai ou juin 1643, in Mersenne, Correspondance, XII, p. 201 sq. ; Lettre de Roberval à Mersenne de juillet 1643, ibid., p. 252 sq. ; Lettre de Torricelli à Roberval du 1er octobre 1643, ibid., p. 328 sq. ; Lettre de Torricelli à Ricci du 17 janvier 1645, ibid., XIII, p. 328 sq. ; Lettre de Roberval à Torricelli du 1er novembre 1645-1er janvier 1646, ibid., XIV, p. 1 sq. ; Lettre de Torricelli à Roberval du 7 juillet 1646, ibid., p. 341 sq. ; Lettre ouverte de Roberval à Torricelli de 1647, ibid., XV, p. 602 sq. On peut aussi trouver ces textes dans les Opere de Torricelli et dans les Mémoires de l’Académie royale des sciences depuis 1666 jusqu’à 1699, t. VI, Paris, Compagnie des libraires, 1730.
L’opuscule de Fermat Sur la transformation et la simplification des équations de lieux pour la comparaison de toutes les formes des aires curvilignes, soit entre elles, soit avec les rectilignes et en même temps sur l’emploi de la progression géométrique pour la quadrature des paraboles et des hyperboles à l’infini, in Œuvres de Fermat, III, p. 216 sq. fait une démonstration analogue sur l’espace compris dans un segment d’hyperbole DEGR qui s’étend à l’infini vers la droite.

Enfin, certaines lignes offrent le même paradoxe.
C’est le cas de la spirale géométrique que Torricelli présente dans une lettre du 7 juillet 1646. Soit un segment AB divisé en C ; on élève la perpendiculaire CD telle que
![]()
ou CD2 = BC . CA
Puis on divise l’angle DCA par CE en deux angles égaux de manière à avoir de nouveau
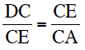
ou CE2 = DC . CA
Et ainsi de suite : CF, qui divise DCE en deux angles égaux, est défini par
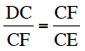
ou CF2 = DC . CE
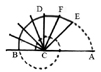
Si l’on multiplie ainsi les rayons issus du centre C et si l’on joint les extrémités, on engendre une spirale qui présente la particularité de s’enrouler indéfiniment autour de C sans jamais l’atteindre : « antequam perveniat ad centrum, infinitas revolutiones circa ipsum absolvere debebit ». Sur cette spirale dite aujourd’hui logarithmique, voir Petite encyclopédie des mathématiques, Didier, 1980, p. 481. Descartes s’est également intéressé à la spirale logarithmique, quoique sa nature l’exclue du domaine de la géométrie qu’il juge légitime : voir Belaval Yvon, Leibniz critique de Descartes, p. 309 sq., et Vuillemin Jules, Mathématiques et métaphysique chez Descartes, p. 39 sq.
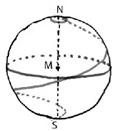
Roberval remarque que la spirale en question n’est autre que la transposition sur le plan de la ligne dite « loxodromie », « seu ventorum via », c’est-à-dire la route que suit, sur le globe terrestre, un vaisseau dont la course coupe tous les méridiens sous le même angle : elle aussi s’enroule en une infinité de circonvolutions autour du pôle, qui tient lieu de point asymptotique, et elle aussi a une mesure finie. Voir la lettre de Mersenne à Peiresc du 26 juillet 1634, Mersenne Marin, Correspondance, IV, p. 264 sq. ; référence à Harmonie universelle, Livre second, Du mouvement des corps, éd. CNRS, t. I, p. 113 sq., Propositions VIII et IX.