Pensées de Blaise Pascal

Rechercher :

Fragment Grandeur n° 6 / 14 – Papier original : RO 191-1

Copies manuscrites du XVII^e s. : C₁ : Grandeur n° 148 à 151 p. 37bis v° à 39 / C₂ : p. 58 à 60

Éditions de Port-Royal : Chap. XXI - Contrarietez estonnantes... : 1669 et janv. 1670 p. 160-162 / 1678 n° 1 p. 158-160 ;

Chap. XXVIII - Pensées Chrestiennes : 1669 et janv. 1670 p. 244-245 / 1678 n° 15 p. 236-237

Éditions savantes : Faugère II, 108, XXIX / Havet VIII.6 / Michaut 420 / Brunschvicg 282 / Tourneur p.195-1 / Le Guern 101 / Lafuma 110 / Sellier 142

_________________________________________________________________________________________

Bibliographie ✍

Concept de cœur : voir la bibliographie dans le dossier sur le cœur.

Théorie de la connaissance

ADORNO Francesco Paolo, Pascal, Les Belles Lettres, Paris, 2000, 144 p.

ALEXANDRESCU Vlad, Le paradoxe chez Blaise Pascal, Peter Lang, Berne-Berlin-Francfort, 1997, 262 p.

BAUDIN Emile, La Philosophie de Pascal, La Baconnière, Neuchâtel, 1946-1947, 4 vol. (1. Pascal et Descartes ; 2. Pascal, les libertins et les jansénistes (2 vol.) ; 3. Pascal et la casuistique).

BLANCHE Robert, Introduction à la logique contemporaine, A.Colin, Paris, 1968, 206 p.

BOUCHILLOUX Hélène, “La méthode démonstrative comme résidu de l’art de persuader”, in MEURILLON Christian (dir.), Pascal, l’exercice de l’esprit, Revue des sciences Humaines, 244, décembre 1996, p. 117-137.

BRUNSCHVICG Léon, Spinoza et ses contemporains, Alcan, Paris, 1923, 496 p.

CHAIX-RUY Jules, “La notion de structure chez Pascal”, Giornale di Metafisica, t. XVII, 6, 1962, p. 581-589.

CHEVALIER Jacques,“La méthode de connaître d’après Pascal”, in Etudes sur Pascal, Revue de Métaphysique et de Morale, 1923, p. 53-86.

COUSIN Victor, “Le scepticisme de Pascal”, Revue des deux mondes, 15 fév. 1844, p.1012-1033, et 15 janv. 1845, p.333-357.

DROZ Edouard, Essai sur le scepticisme de Pascal considéré dans le livre des Pensées, Alcan, Paris, 1886, 394 p.

DUCAS A., “La pensée et la connaissance de Pascal”, Méditerranée vivante, Imbert, Alger, 1952, 152 p.

FLOTTES, “Du reproche de scepticisme fait à Pascal. Lettre adressée au rédacteur de L’Ami de la Religion, datée de Montpellier, 2 août 1847”, L’Ami de la religion, 26 août 1847, p. 481-486.

GOODHUE W.W., “Pascal's theory of knowledge : a reaction to the analytical method of Descartes”, Modern Schoolman, t. XLVII, 1, 1969-1970, p. 15-35.

McKENNA Antony, “Deux termes-clefs du vocabulaire pascalien : idée et fantaisie”, in MEURILLON Christian (dir.), Pascal, l’exercice de l’esprit, Revue des Sciences Humaines, 244, décembre 1996, p.103-116.

MEURILLON Christian, “Mémoire et vérité : itinéraire pascalien”, in MEURILLON Christian (dir.), Pascal, l’exercice de l’esprit, Revue des Sciences Humaines, 244, décembre 1996, p. 139-157.

PELET P., Le scepticisme de Pascal, Chauvin et fils, Toulouse, 1871.

PERDOMO José, La teoria del conocimento en Pascal : filosofia critica pascaliana, Consejo superior de investigaciones cientificas, Madrid, 1956.

PETITOT H., “La théorie de la connaissance chez Pascal”, Revue thomiste, août 1909.

POPKIN Richard, Histoire du scepticisme d’Erasme à Spinoza, Presses Universitaires de France, Paris, 1979, 342 p.

PRIGENT Jean, “La notion d’ordre chez Pascal”, in Ordre, désordre, lumière, Vrin, Paris, p. 190-209.

SAISSET E., Le scepticisme, Aenesidème, Pascal, Kant, Didier, Paris, 1865, XVI-464 p.

SHIOKAWA Tetsuya, “Justus ex fide vivit et fides ex auditu : deux aspects de la foi dans l’apologétique pascalienne”, in MEURILLON Christian (dir.), Pascal, l’exercice de l’esprit, Revue des Sciences Humaines, 244, 1996, p. 159-178.

SHIOKAWA Tetsuya, “La connaissance par l’autorité selon Pascal”, Etudes de langue et littérature françaises, n° 30, 1977, p.1-14.

SHIOKAWA Tetsuya, “La raison et l’autorité dans les études patristiques : le cas de Pascal et de la Logique de Port-Royal”, in Les Pères de l’Eglise au XVII^e siècle, Cerf, 1993.

SPOERRI Théodule, “Les pensées de derrière la tête de Pascal”, in Pascal, l’homme et l’œuvre, Cahiers de Royaumont, Minuit, Paris, 1956, p. 386-429.

✧ Éclaircissements

Nous connaissons la vérité non seulement par la raison mais encore par le cœur, c’est de cette dernière sorte que nous connaissons les premiers principes et c’est en vain que le raisonnement, qui n’y a point de part, essaie de les combattre. Les pyrrhoniens, qui n’ont que cela pour objet, y travaillent inutilement. Nous savons que nous ne rêvons point, quelque impuissance où nous soyons de le prouver par raison ; cette impuissance ne conclut autre chose que la faiblesse de notre raison, mais non pas l’incertitude de toutes nos connaissances, comme ils le prétendent

L'édition Lafuma donne un texte assez différent pour la lettre et pour le sens : « Nous connaissons la vérité non seulement par la raison mais encore par le cœur. C'est de cette dernière sorte que nous connaissons les premiers principes et c'est en vain que le raisonnement, qui n'y a point de part essaie de les combattre. Les pyrrhoniens, qui n'ont que cela pour objet, y travaillent inutilement. Nous savons que nous ne rêvons point. Quelque impuissance où nous soyons de le prouver par raison, cette impuissance ne conclut autre chose que la faiblesse de notre raison, mais non pas l'incertitude de toutes nos connaissances, comme ils le prétendent. »

Sellier Philippe, Pascal et saint Augustin, p. 44, présente ce fragment comme le Contra Academicos de Pascal, c’est-à-dire comme le texte dans lequel il réunit ses principaux arguments contre le scepticisme. Voir aussi p. 537 sq., sur l’activité de connaissance du cœur.

Miel Jan, Pascal and theology, p. 165 sq. effectue le rapprochement avec L’esprit géométrique sur les principes et les notions primitives, et avec les premières lignes du fragment Preuves par discours I (Laf. 418, Sel. 680), “Infini rien”.

Gouhier Henri, Blaise Pascal. Conversion et apologétique, p. 63 sq., pense que l’intention générale de ce texte ne relève pas de la réflexion épistémologique sur la théorie de la connaissance, mais plutôt de la partie ratiocinante de l’apologétique. Pascal veut souligner et exploiter une analogie : en religion comme en géométrie, la raison ne rend pas compte de tout.

Nous savons que nous ne rêvons point : voir Contrariétés 14 (Laf. 131, Sel. 164), sur l’argument sceptique du rêve : Personne n’a d’assurance, hors de la foi, s’il veille ou s’il dort, vu que durant le sommeil on croit veiller aussi fermement que nous faisons. On croit voir les espaces, les figures, les mouvements, on sent couler le temps, on le mesure, et enfin on agit de même qu’éveillé. De sorte que la moitié de la vie se passant en sommeil, par notre propre aveu ou quoi qu’il nous en paraisse, nous n’avons aucune idée du vrai, tous nos sentiments étant alors des illusions. Qui sait si cette autre moitié de la vie où nous pensons veiller n’est pas un autre sommeil un peu différent du premier, et dont nous nous éveillons quand nous pensons dormir, comme on rêve souvent, qu’on rêve entassant un songe sur l’autre.

Shiokawa Tetsuya, “Justus ex fide vivit et fides ex auditu : deux aspects de la foi dans l’apologétique pascalienne”, in Meurillon Christian (dir.), Pascal, l’exercice de l’esprit, Revue des sciences Humaines, 244, 1996, p.159-178. Voir p. 175 sur ce texte. ✍

♦ Par la raison

Sellier Philippe, Port-Royal et la littérature, I, Pascal, p. 223 sq. “La dérision de la raison”. La force de la raison : p. 224. ✍

♦ Qu’est-ce que le cœur ?

Pascal ne donne pas de définition précise de la nature de ce qu’il entend par cœur. Les commentateurs ont tenté de pallier ce manque.

Lire le dossier thématique sur le cœur...

Car la connaissance des premiers principes, comme qu’il y a espace, temps, mouvement, nombres, est aussi ferme qu’aucune de celles que nos raisonnements nous donnent et c’est sur ces connaissances du cœur et de l’instinct qu’il faut que la raison s’appuie et qu’elle y fonde tout son discours

♦ Le cœur et les principes

Les connaissances que le cœur fournit par le sentiment constituent les principes sur lesquels se fonde tout le raisonnement rationnel.

✍

Mesnard Jean, Les Pensées de Pascal, 2^e édition, Paris, SEDES-CDU, 1993, p. 94. Le cœur est la faculté des principes.

Sellier Philippe, Pascal et saint Augustin, p. 537. L’activité de connaissance du cœur.

Lacombe Roger, L’apologétique de Pascal, p. 43 sq.

Gouhier Henri, Blaise Pascal. Conversion et apologétique, p. 62, sur le cœur qui sent qu’il y a trois dimensions. Comparaison avec la manière dont L’esprit géométrique parle de la connaissance des principes et L’art de persuader du cœur : p. 60. Dans le fragment Laf. 110, la connaissance des premiers principes est expressément rapportée au cœur : p. 62. Et comme ce texte associe expressément cœur et principes, M. Henri Gouhier, en vrai philosophe, conclut, p. 65, qu’il n’y a aucune correspondance entre cœur et principe, et fait du fragment un texte purement apologétique sur l’analogie entre l’indémontrable en géométrie et l’indémontrable en matière religieuse. C’est une démarche très philosophique de se débarrasser d’un texte sous prétexte qu’il est unique parce qu’on le trouve gênant.

♦ Les connaissances du cœur, fondement de tout le raisonnement

C’est à partir des principes fondamentaux fournis par le cœur que la raison peut déduire des conséquences.

Laf. 530, Sel. 455. Tout notre raisonnement se réduit à céder au sentiment.

Silhon Jean de, De l’immortalité de l’âme, Paris, Pierre Billaine, 1634, Discours II, Qu’il est nécessaire de montrer qu’il y a un Dieu pour prouver l’immortalité de l’âme. Réfutation du pyrrhonisme et des raisons que Montaigne apporte pour l’établir. Divers genres de démonstration [...], p. 117. Lorsqu’il s’agit d’invoquer des propositions connues et admises par tous, Silhon cite des principes de la métaphysique que des mathématiques à côté d’axiomes mathématiques euclidiens : « qu’il est impossible qu’une même chose soit et ne soit pas en même temps. Que tout être est nécessaire ou contingent, c’est-à-dire que tout ce qui est ou tient son être de soi ou l’a reçu. Que le tout est plus grand que chacune des parties qui le composent ; que qui ôtera de deux quantités semblables des portions égales ou des nombres pareils, ce qui restera sera égal ou pareil ».

- Le cœur sent qu’il y a trois dimensions dans l’espace

Pascal écrit dans son l’Introduction à la géométrie, Mesnard Jean, OC III, p. 435, que « l’objet de la pure géométrie est l’espace, dont elle considère la triple étendue en trois sens divers qu’on appelle dimensions, lesquelles on distingue par les noms de longueur, largeur et profondeur, en donnant indifféremment chacun de ces noms à chacune de ces dimensions, pourvu qu’on ne donne pas le même à deux ensemble. Elle suppose que tous ces termes-là sont connus d’eux-mêmes ».

Pour approfondir (Trois dimensions dans l’espace)...

et que les nombres sont infinis

Preuves par discours I (Laf. 418, Sel. 680). Infini rien.

Notre âme est jetée dans le corps où elle trouve nombre, temps, dimensions, elle raisonne là-dessus et appelle cela nature, nécessité, et ne peut croire autre chose.

L’unité jointe à l’infini ne l’augmente de rien, non plus que un pied à une mesure infinie ; le fini s’anéantit en présence de l’infini et devient un pur néant. Ainsi notre esprit devant Dieu, ainsi notre justice devant la justice divine. Il n’y a pas si grande disproportion entre notre justice et celle de Dieu qu’entre l’unité et l’infini.

Il faut que la justice de Dieu soit énorme comme sa miséricorde. Or la justice envers les réprouvés est moins énorme et doit moins choquer que la miséricorde envers les élus.

Nous connaissons qu’il y a un infini, et ignorons sa nature comme nous savons qu’il est faux que les nombres soient finis. Donc il est vrai qu’il y a un infini en nombre, mais nous ne savons ce qu’il est. Il est faux qu’il soit pair, il est faux qu’il soit impair, car en ajoutant l’unité il ne change point de nature. Cependant c’est un nombre, et tout nombre est pair ou impair. Il est vrai que cela s’entend de tout nombre fini.

Précision intéressante, dans la mesure où elle explique comment on sait que le cœur sent que les nombres sont infinis : il se rend compte immédiatement qu’il est impossible qu’il s’arrête, et sa certitude est purement négative ; c’est la certitude d’une fausseté, et, du point de vue pratique, d’une impuissance. Et la conclusion positive, les nombres sont infinis, est tirée par contradiction. Ou les nombres sont finis, ou ils ne le sont pas ; il n’y a pas de tiers ; or ils ne sont pas finis, donc ils sont infinis. On a fait d’une évidence négative un énoncé positif.

Pour approfondir...

♦ L’infinité des nombres

C’est un des axiomes ajoutés à Euclide VII, à titre de postulat. Axiome 2 : on peut prendre un nombre plus grand que tout nombre donné. Axiome 3 : la suite des nombres peut se poursuivre à l’infini. Le premier est donné dans Hérigone, Cursus, I, p. 265. Cela remonte à Campanus et appartient donc à la tradition mathématique.

Voir le cas des nombres premiers dans Euclide, Eléments, IX, 20, éd. Vitrac, Paris, Presses Universitaires de France, t. 2, p. 444. Les nombres premiers sont plus nombreux que toute multitude de nombres premiers proposés.

De même que l’affirmation selon laquelle l’espace a trois dimensions, celle que l’infinité des nombres est une évidence du cœur peut être discutée, et certains mathématiciens ont essayé de la démontrer. Voir Patrizzi, qui consacre une partie de sa Géométrie à prouver ce que Pascal présente ici comme un principe.

On pourrait discuter cette attribution au cœur de la connaissance de l’infinité des nombres et la présenter comme un raisonnement à partir des Postulats II et III de Hérigone. Principe : l’addition des nombres est possible. Principe : à tout nombre donné on peut en prendre un plus grand. Par conséquent à tout nombre donné on peut en trouver un plus grand par addition ; par suite l’addition des nombres peut se poursuivre à l’infini.

Dans L’esprit géométrique, I, De la géométrie en général, § 23, Mesnard Jean, OC III, p. 402, Pascal n’envisage pas directement le nombre infini ; il souligne seulement qu’on n’atteint jamais un nombre infini par accroissement progressif. Encore ne parle-t-il pas de nombre infini, mais de nombre qui ne peut pas être augmenté, c’est-à-dire de plus grand nombre. Il reste à établir que ce plus grand nombre est un nombre infini. Il est clair par ce que dit Pascal qu’il ne peut pas être fini. Dès lors, on ne voir pas bien ce qu’il pourrait être d’autre qu’infini. « De même, quelque grand que soit un nombre, on peut en concevoir un plus grand, et encore un qui surpasse le dernier ; et ainsi à l’infini, sans jamais arriver à un qui ne puisse plus être augmenté. Et au contraire, quelque petit que soit un nombre, comme le centième ou la dix millième partie, on peut encore en concevoir un moindre, et toujours à l’infini, sans arriver au zéro ou néant. »

L’existence du nombre infini est clairement affirmée dans le fragment Laf. 663, Sel. 544. La nature recommence toujours les mêmes choses, les ans, les jours, les heures, les espaces de même. Et les nombres sont bout à bout, à la suite l’un de l’autre ; ainsi se fait une espèce d’infini et d’éternel. Ce n’est pas qu’il y ait rien de tout cela qui soit infini et éternel, mais ces êtres terminés se multiplient infiniment. Ainsi il n’y a ce me semble que le nombre, qui les multiplie, qui soit infini. Pascal y affirme nettement que le nombre infini est sans doute le seul infini réel, tous les autres n’en étant que le produit. Mais il précise le nombre « qui les multiplie » : il pense donc au nombre en tant qu’opérateur.

Le nombre infini invoqué en exemple du fait que tout ce qui est incompréhensible ne laisse pas d’être dans le fragment A P. R. 2 (Laf. 149, Sel. 182).

Sur l’infini en nombre, voir le fragment Preuves par discours I (Laf. 418, Sel. 680).

Certains mathématiciens et philosophes estiment que le nombre infini n’a pas d’existence réelle. Voir par exemple Duhem Pierre, Le système du monde, VII, p. 119. Jean de Bassols contre Aristote qui nie le nombre actuellement infini.

et la raison démontre ensuite qu’il n’y a point deux nombres carrés dont l’un soit double de l’autre.

Il n’est pas possible de trouver un carré double d’un autre carré.

Voir L’Esprit géométrique, Mesnard Jean, OC III, p. 405, où Pascal déclare cette proposition trop facile pour valoir une démonstration, et se contente de l’illustrer par le défi de former un carré double d’un autre en disposant des points en carré.

Pour approfondir…

♦ Duplication d’un carré

Le problème n’est pas neuf. Voir Szabó Árpád, L’aube des mathématiques grecques, Vrin, Paris, 2000, 368 p. Voir p. 154 sq., sur le problème de la duplication du carré. Socrate et le problème arithmétique de la duplication du carré dans le Ménon, 82 b-85 e : p. 154-155. Dans la représentation des nombres par des figures géométriques, il n’y a que le carré que l’on peut représenter par une figure géométrique. Le problème arithmétique de la duplication du carré revient à se demander si le produit de la duplication d’un nombre carré est encore un nombre carré : p. 155. Proclus l’énonce comme suit : « un nombre carré n’est pas le double d’un autre nombre carré » : p. 155. Référence : Procli Diadochi in rempublicam Platonis, éd. G. Kroll, Lipsiae, 1901, p. 27.

Voir une reconstitution de la démonstration dans Hogben Launcelot, Les mathématiques pour tous, p. 201 sq., qui mentionne la proposition d’Euclide sur la diagonale, mais son exposé est fait en termes numériques.

On doit avoir : m² = 2 n²

Soit en tirant la racine :

On cherche les deux carrés, en supposant cette fraction réduite à sa plus simple expression. Mais si m et n sont pairs, on diviserait le rapport par 2, et la fraction ne serait pas réduite à sa plus simple expression ; donc on a nécessairement

soit m impair,

soit n impair,

soit m et n impairs.

En prenant l’égalité m² = 2 n², on voit immédiatement que dans , le numérateur est forcément pair, car

un nombre impair a un carré impair,

or 2 n² ne peut pas être impair,

donc m² est pair,

donc m est pair.

D’autre part, si l’on fait , en remplaçant m par 2 p, on aura

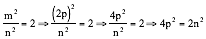
et au bout du compte :

2 p² = n²ou

Donc pour les mêmes raisons que ci-devant, n² est pair, donc n est pair aussi.

Donc les prémisses supposent m et n impairs, et les conclusions les donnent pairs. Donc la supposition initiale est impossible, et il n’y a pas deux carrés dont l’un soit double de l’autre.

En deux mots... Si , point de départ, est réduite à sa plus simple expression, m et n ne peuvent pas être pairs à la fois (on pourrait diviser le rapport par 2) ; mais avec , ils doivent l’être. Donc il n’y a pas de fraction dont le carré est égal à 2.

Brunschvicg Léon, Les étapes de la philosophie mathématique, p. 47 sq.

♦ Le manuscrit porte en partie barrée une référence au théorème de Pythagore sur le carré de l’hypoténuse

Voir ce théorème dans Euclide, Eléments, I, Proposition 47, éd. Heath, t. 1, p. 349 sq.

Pour approfondir...

♦ Théorème de Pythagore

Rien n’atteste que le théorème qui porte son nom soit effectivement dû à Pythagore : voir Heath Thomas, A history of greek mathematics, I, p. 144 sq.

Rey Abel, La Science dans l’Antiquité, V, L’apogée de la science technique grecque, p. 208-209. La démonstration est due à Euclide, et n’est ni celle des Pythagoriciens, ni aucune de celles de la géométrie antérieure ; Euclide a dû la chercher pour ne pas présupposer des propositions ultérieures et préserver l’ordre logique.

Greek mathematical works, I, éd. Ivor Thomas, p. 178 sq. La démonstration par Pythagore devait procéder par sa théorie inadéquate des proportions, qui ne s’appliquait qu’aux grandeurs commensurables. Lorsque les incommensurables furent découvertes, il fallut trouver une preuve nouvelle, indépendante des proportions ; c’est ce que fait Euclide.

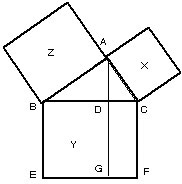
Or par Livre III, Section II, Proposition II, 18. Si une ligne droite est coupée comme l’on voudra, les rectangles compris de la toute, et de chacune de ses parties, sont égaux au carré de la toute.

Arnauld et Nicole, La Logique, IV, IX, 4^e défaut, Démonstrations tirées par des voies trop éloignées. « La 47. du 1^er livre, où il est prouvé que le carré de la base qui soutient un angle droit, est égal au carré des côtés, est une des plus estimées propositions d’Euclide. Et néanmoins il est assez clair que la manière dont elle y est prouvée n’est point naturelle, puisque l’égalité de ces carrés ne dépend point de l’égalité des triangles qu’on prend pour moyen de cette démonstration, mais de la proportion des lignes qu’il est aisé de démontrer, sans se servir d’aucune autre ligne que de la perpendiculaire du sommet de l’angle droit sur la base. Tout Euclide est plein de ces démonstrations par des voies étrangères. »

Arnauld donne une présentation originale. Voir Nouveaux Eléments de géométrie, Livre XV, Second théorème, XXXI, in Géométries de Port-Royal, éd. D. Descotes, p. 754. Si l’on construit sur l’hypoténuse et sur les deux côtés d’un angle droit des figures semblables quelconques, celle qui sera construite sur l’hypoténuse sera égale aux deux qui seront construites sur les côtés. C’est la généralisation de la proposition sur le carré de l’hypoténuse.

Les principes se sentent, les propositions se concluent et le tout avec certitude quoique par différentes voies - et il est aussi inutile et aussi ridicule que la raison demande au cœur des preuves de ses premiers principes pour vouloir y consentir, qu’il serait ridicule que le cœur demandât à la raison un sentiment de toutes les propositions qu’elle démontre pour vouloir les recevoir.

♦ Critique de la manie destructrice des sceptiques

Comme, selon le fragment Preuves par discours I (Laf. 423, Sel. 680), le cœur a ses raisons que la raison ne connaît pas, l’exigence de démonstration totale qui inspire les sceptiques et pyrrhoniens a quelque chose de tyrannique, au sens des fragments Misère 6 (Laf. 58, Sel. 91) et Misère 7 (Laf. 58, Sel. 92), en ce sens que c’est demander au cœur ce qu’il ne peut donner, et que seule la raison pourrait fournir, si elle était capable de prouver les principes. Pascal entreprend donc ici une critique par l’argument d’hétérogénéité, de la manie sceptique qui consiste à demander compte de tout comme d’une forme d’hyperrationalisme. La manie de demander des preuves de tout, qui caractérise le scepticisme, est mal placée à partir du moment où elle conduit à demander des démonstrations là où il n’y a pas lieu d’en donner.

En fait, sur ce point, les mathématiciens ont parfois imité les sceptiques.

Pour approfondir...

♦ Les mathématiciens ont parfois imité les sceptiques

Szabó Árpád, Les débuts des mathématiques grecques, p. 248. Sur les tentatives d’Apollonius pour démontrer l’axiome d’égalité.

Ramus Pierre, Petri Rami Veromandui philosophi celeberrimi, eloquentiae et mathematicarum disciplinarum professoris regii Scholarum mathematicarum libri unus et triginta, dudum a Lazaro Schonero recogniti et aucti, nunc vero in postrema hac editione innumeris locis emendati et locupletati, Livre III, sur les tentatives de démonstration excessives, comme quand Apollonius cherche à montrer que les choses égales à une même sont égales entre elles : p. 89. « Ego vero ista consideranti non dubito furoris similem ambitionem in tam multorum principiorum demonstrationibus visum iri. Attamen furor iste animi eo pervasit, ut sol ille in mathematicis elementis clarissimus, Quae eidem aequalia, etiam demonstrabilis visus sit. Apollonius enim alioqui praestantissimus author, demonstrare tentavit, quem videlicet aemulatus esse dicitur Regiomontanus, ingenio fortasse nihil inferior. Prima siquidem arithmeticae elementa de additione, subductione, multiplicatione, divisione, Euclidis theorematis demonstrare conatus est, indeque algorithmus ab eo creditur esse demonstratus : qui morbus ignavis et inertibus ingeniis accidere non potest, sed generosis tantum mentibus, tanquam victa quavis oblata rerum difficultate, olympicum aliquod praemium expetentibus. Morbus tamen est gravissimus, cujus contagione nobilissimas disciplinas ad interitum pené redactas animadvertimus : principia namque sumenda et postulanda, caetera autem ex iis demonstranda [...]. Hoc igitur primum in demonstrationibus sophisma est obscuritatis immensae, quo principia demonstrantur, quo hypotheses, id est definitiones, partitiones, quo postulata demonstrantur, quantum erit et quantae obscuritatis sophisma, quo syllogismi positis antecedentibus, complexiones demonstrantur ? » : p. 89. Voir Livre VII, in postulata et axiomata, p. 154 sq. Quae eidem sunt aequalia, et inter se sunt aequalia : p. 156. Axioma est catholicum. « Hoc axioma omnium axiomatum, ut ordine sic usu primum est. [...] Nec Euclides alligavit proprie aut numeris aut magnitudinibus, sed omnium rerum fecit commune, cum isto modo proposuit, ut etiam septem deinceps alia proposuit : sed axioma hoc primum utilitatis est immensae. Algebra contemplationes arithmeticas singulares habet, at summa contemplationum earum axiomate isto continetur : hinc enim est aequatio, comparatio nempe in quantitate, qua figurati diversi et affirmati secundum hypothesim inter se ideo aequantur, quia eidem tertio aequantur : hinc aequationis et genera et species... » Cet axiome est très utile, mais il est si connu qu’on ne le voit même plus. Apollonius a essayé de montrer que c’est une proposition et non un principe. « Sit enim (ait) a aequale ipsi b, et b aequale ipsi c, dico quod etiam a ipsi c aequale est. Cum enim a ipsi b aequale sit, eundem occupat locum, quem b, et quoniam b ipsi c aequale est, eundem quem et ipsum occupat locum, quel c, aequalia igitur. Sic igitur Apollonius axioma primum demonstrasse visum est. Verumtamen primum non satis attendit, quo argumento quam quaestionem concluderet. Quae (ait) eidem tertio sunt aequalia, inter se sunt aequalia, quyia eundem locum occupant ; Haec Apollonii caussa est. At (inquam) ista caussa specialis est, et geometrica tantum : logica enim aequalitatis ratio, loci mensura nulla continetur. Quare axioma, Quae eidem aequalia, inter se aequalie, multo altius est geometrico axiomate, Quae eundem locum occupant, sunt aequalia, nec ideo speciale principium, generalis prinncipii caussa est, unde sequitur ab Apollonio postulari quod erat in principio, ut Aristoteles loquitur, non autem demonstrari » : p. 156.

Cette impuissance ne doit donc servir qu’à humilier la raison, qui voudrait juger de tout,

La rétorsion est équilibrée : elle humilie la raison, ce qui est conforme au christianisme, et seulement dans la mesure où elle est tyrannique ; mais elle laisse intacte la capacité de certitude venue du cœur (ce qui épargne la grâce).

✍

Sellier Philippe, Port-Royal et la littérature, I, Pascal, p. 223 sq. “La dérision de la raison”. La force de la raison : p. 224.

Gouhier Henri, Blaise Pascal. Conversion et apologétique, p. 64. Intention apologétique visible de ce texte visible par le mot humilier, absent de L’Esprit géométrique : p. 64.

Laporte Jean, Le cœur et la raison selon Pascal, p. 13 sq. La corruption de l’intelligence selon Port-Royal n’est pas complète : la raison n’est corrompue qu’en tant qu’elle est soumise à la volonté : p. 15 sq. Mais dans les sciences mathématiques et physiques, Pascal reproche à Descartes l’excès de son dogmatisme rationaliste plutôt que son mécanisme en physique: p. 20 sq. Comme le montre le fragment “Disproportion de l’homme”, l’infinité des sciences dépasse la raison : p. 24 sq.

mais non pas à combattre notre certitude, comme s’il n’y avait que la raison capable de nous instruire ; plût à Dieu que nous n’en eussions au contraire jamais besoin et que nous connaissions toutes choses par instinct et par sentiment, mais la nature nous a refusé ce bien ; elle ne nous a au contraire donné que très peu de connaissances de cette sorte, toutes les autres ne peuvent être acquises que par raisonnement.

Giocanti Sylvia, Penser l’irrésolution..., p. 137. L’impuissance de la raison à démontrer les principes ne remet pas en cause la validité de ces principes ; elle ne peut servir qu’à donner une leçon à la raison qui a tendance à s’aventurer là où elle n’a que faire, leçon que la raison s’obstine à ne pas comprendre.

La certitude des principes du cœur ne tient pas à une garantie d’ordre métaphysique, comme on le voit chez Descartes. Il n’y a pas de preuve des principes, et en cela les sceptiques ont raison. Dans A P. R., Pascal écrit que l’homme n’est assuré de ne pas dormir et de ne pas rêver que par la foi, ce qui excède évidemment la philosophie et les démonstrations rationnelles.

Mais cette certitude vient en fait de ce que l’homme, fait comme il est, ne peut penser autrement que par ces notions que le cœur lui fournit. Comme l’indique le fragment “Infini rien”, Preuves par discours I (Laf. 418, Sel. 680), Notre âme est jetée dans le corps où elle trouve nombre, temps, dimensions, elle raisonne là-dessus et appelle cela nature, nécessité, et ne peut croire autre chose.

♦ Double portée, dogmatique et sceptique de l’idée de cœur

La notion de cœur apparaît dans Grandeur, parce qu’elle permet de mettre en lumière des idées dont l’esprit ne peut pas douter, et qui sont donc certaines pour lui.

Mais on peut aussi la tirer dans le sens du scepticisme, car ces notions ne sont appuyées sur rien qui soit métaphysiquement certain.

Un procédé comme celui de la Raison des effets peut être appliqué à ce concept, pour le tirer en un sens ou en l’autre.

Et c’est pourquoi ceux à qui Dieu a donné la religion par sentiment du cœur sont bien heureux et bien légitimement persuadés,

Ce passage annonce les développements de Conclusion sur la foi par sentiment et la foi du charbonnier.

✍

Lacombe Roger, L’apologétique de Pascal, p. 41. La conception de la foi qui découle de ce passage est celle de la foi comme connaissance par le cœur : p. 46.

Sellier Philippe, Port-Royal et la littérature, II, p. 12.

Sellier Philippe, Pascal et saint Augustin, p. 537.

Kolakowski Leszek, Dieu ne nous doit rien, Brève remarque sur la religion de Pascal et l’esprit du jansénisme, p. 193 sq.

Mais ceux qui ne l’ont pas, nous ne pouvons la donner que par raisonnement en attendant que Dieu la leur donne par sentiment de cœur, sans quoi la foi n’est qu’humaine et inutile pour le salut.

Shiokawa Tetsuya, “La connaissance par l’autorité selon Pascal”, Études de langue et littérature françaises, n° 30, 1977, p. 1-14. Voir p. 10. Le but de l’Apologie est de susciter la foi humaine en l’autorité-crédibilité de ce qui témoigne de la religion chrétienne.

♦ La foi humaine, foi obtenue par la raison

Sur la foi humaine, voir Conclusion 4 (Laf. 380, Sel. 412), et les notes connexes.

Shiokawa Tetsuya, “La connaissance par l’autorité selon Pascal”, Études de langue et littérature françaises, n° 30, 1977, p. 1-14. Voir p. 10.✍

Tavard Georges, La tradition au XVII^e siècle, Paris, Cerf, 1969, p. 94. Distinction entre foi divine et foi humaine.✍

Laporte Jean, La doctrine de Port-Royal, La morale, II, p. 409 sq. La foi est la croyance fondée sur l’autorité du témoignage d’autrui. Elle est humaine si ce sont les hommes qui sont à sa source.

Harrington Thomas, Vérité et méthode, p. 118. La foi humaine fait croire par raisonnement, elle ne transforme pas le cœur et ne modifie pas son esclavage à la concupiscence ; la foi divine fait croire les vérités chrétiennes par sentiment du cœur ; elle comporte l’humiliation ; c’est un don gratuit de Dieu qui effectue une conversion. La foi humaine est figure de la foi divine : p. 119. Elle peut en être l’instrument.

Orcibal Jean, La spiritualité de Saint-Cyran, p. 72 sq. Saint Grégoire : la démonstration de l’esprit et d’une preuve convaincante détruit le mérite de la foi ; a fortiori la démonstration des yeux et des sens.

Arnauld Antoine et Nicole Pierre, La logique, IV, XVII, éd. Clair et Girbal, p. 335 sq. De ce que nous connaissons par la foi, soit humaine, soit divine.✍

Arnauld Arnauld, Réflexions d’un docteur de Sorbonne sur l’avis donné par Mgr. l’évêque d’Alet, 1657, Œuvres, XXI, p. 21.✍

♦ La foi divine

Sur la foi divine, voir Conclusion 4 (Laf. 380, Sel. 412), et les notes connexes.

Les dessins en marge du fragment

Ces dessins sont-ils de la main de Pascal ?

Que représentent ces dessins ?

S’agit-il d’un seul dessin, ou de deux dessins séparés ?

ou deux dessins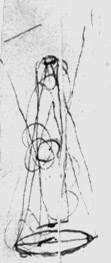

Pour la première image, K. Koyanagi envisage les coniques et les siphons. On peut en effet rapprocher le dessin de celui d’un cône dont la base serait le cercle. Mais il semble bien que les deux verticales de ce cône aient une épaisseur, ce qui se conçoit difficilement en géométrie.

Le rapprochement avec le siphon provient de certaines représentations qui se trouvent dans les livres de physique. On peut renvoyer aux figures de Guiffart, et de Hérigone, par exemple.

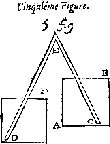
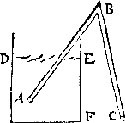
Mais il faut remarquer que Mersenne ne représente presque jamais un siphon sous cette forme, mais toujours recourbé. On ne voit pas bien du reste à quoi correspond, dans ce cas, le cercle de base.

La première image représente peut-être un compas de mesure de distance. En géométrie, le compas sert moins à tracer des cercles qu’à construire des segments rectilignes de longueur égale. Ici, il semble que le segment en question soit le diamètre d’un cercle.

Tourneur pense qu’ils sont en rapport avec la cycloïde.

De fait, la deuxième figure ressemble un peu au rouleau d’Aristote tel qu’il est dessiné dans les planches de la Dissertatio du P. Tacquet. C’est proprement l’instrument qui permet de montrer le paradoxe d’Aristote sur l’identité des distances parcourues par des cercles de circonférence différente. Quant à la roulette, on engendre avec cet instrument des cycloïdes de tous les genres, selon la manière dont s’effectue le roulement.

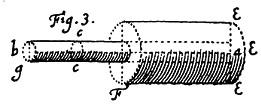
Autant le premier dessin est confus, autant le second semble net et précis ; il comporte même un rendu des ombres.

Dans cette perspective, on peut réinterpréter le premier des deux dessins.

On y trouve le cercle de base, qui est la tête du « clou », qui porte le point mobile. Mais alors que d’habitude, c’est le rapport du rayon de la roue et du cercle porteur qui change, on a l’impression que Pascal envisage ici diverses sortes d’essieux.

L’essieu classique se trouve au centre, à peine esquissé. Mais on voit distinctement que la section est dessinée.

On voit aussi un cône dont la base est le cercle, et dont les deux verticales passent par la section de l’essieu précédent.

Il y a un autre cône, qui passe aussi par une section un peu plus petite, au-dessus. Ce sont ces deux cônes qui donnent l’impression de voir un compas.

Il reste une partie le plus souvent négligée du dessin, le triangle disposé symétriquement aux deux autres, dont une section verticale seule est tracée. Ses verticales passent aussi par la section de l’essieu primitif. Mais il ne semble pas avoir de pointe. Il paraît s’arrêter à la section de l’essieu elle-même.

Bref, je me demande si l’on ne peut pas interpréter ce dessin comme une tentative de généralisation de la roulette, non pas dans le sens de la variation du rapport entre la roue et le cercle porteur, mais de la forme de l’essieu. Un rouleau, comme on le sait par les travaux de Desargues et de Pascal sur les coniques, est un cône dont le sommet est rejeté à l’infini. Que se passe-t-il si le sommet du cône est à distance finie ? Et que se passe-t-il si le sommet du cône coïncide avec le centre du cercle porteur ?

Quand l’essieu est un rouleau, on se trouve dans le cas de la roulette ordinaire, qui est tracée dans un plan. Dans le cas présent, ce serait une roulette raccourcie (au sens de Roberval).