Pensées diverses III – Fragment n° 57 / 85 – Papier original : RO 442-7
Copies manuscrites du XVIIe s. : C1 : n° 136 p. 379 / C2 : p. 339
Éditions de Port-Royal : Chap. XXIX - Pensées morales : 1669 et janvier 1670 p. 286 / 1678 n° 35 p. 283
Éditions savantes : Faugère I, 187, XXVIII / Havet VI.28 / Brunschvicg 180 / Tourneur p. 106-3 / Le Guern 598 / Lafuma 705 (série XXV) / Sellier 583
______________________________________________________________________________________
Bibliographie ✍
BÉNICHOU Paul, Morales du Grand Siècle, Paris, Gallimard, 1948. CARRAUD Vincent, Pascal. Des connaissances naturelles à l’étude de l’homme, Paris, Vrin, 2007. DESCOTES Dominique, Blaise Pascal. Littérature et géométrie, Clermont-Ferrand, Presses Universitaires Blaise Pascal, 2001. MERKER Claude, Le chant du cygne des indivisibles. Le calcul intégral dans la dernière œuvre scientifique de Pascal, Besançon, Presses Universitaires Franc-Comtoises, 2001. MESNARD Jean, Les Pensées de Pascal, Paris, SEDES-CDU, p. 1993. ROBERVAL Gilles Personne de, Traité des mouvements composés, Traité des indivisibles, De Trochoide, etc. in Divers ouvrages de Mathématiques et de Physique par MMrs de l’Académie Royale des Sciences, Paris, Imprimerie Royale, 1693. STIKER-MÉTRAL Charles-Olivier, Narcisse contrarié. L'amour propre dans le discours moral en France (1650-1715), Paris, Champion, 2007. |
✧ Éclaircissements
Les grands et les petits ont mêmes accidents et même fâcherie et même passion, mais l’un est au haut de la roue et l’autre près du centre et ainsi moins agité par les mêmes mouvements.
Le fond du fragment peut être rapproché des idées du mouvement augustinien, et de la manière dont, selon Paul Bénichou, Morales du Grand Siècle, certains moralistes entreprennent de démolir l’idéal moral aristocratique et héroïque. Voir sur ce point ✍
Bénichou Paul, Morales du Grand Siècle, Paris, Gallimard, 1948.
Stiker-Métral Charles-Olivier, Narcisse contrarié. L'amour propre dans le discours moral en France (1650-1715), 2007.
Fâcherie (fascherie) : Colère, chagrin, déplaisir (Furetière).
Accidents : au sens de hasard, coup de fortune (Furetière).
Les singuliers fâcherie et passion sont souvent mis au pluriel par les éditeurs, par attraction avec accidents. C’est la lectio facilior, qu’ont imposée les Copies. En fait le singulier est parfaitement acceptable, si l’on entend même manière de se fâcher, et même manière d’être passionné.
L’idée que les gens du vulgaire sont essentiellement de même nature que les grands, à ceci près que leur situation sociale les expose à de moindres tribulations, est contraire à l’esprit aristocratique et héroïque de la tragédie, notamment dans sa forme cornélienne. En revanche, elle est présente dans les Trois discours sur la condition des grands que Pascal a composés pour l’instruction du duc de Luynes. « Votre âme et votre corps sont d'eux-mêmes indifférents à l'état de batelier, ou à celui de duc ; et il n'y a nul lien naturel qui les attache à une condition plutôt qu'à une autre. »
Voltaire, Lettres philosophiques, XXV, § XXXVIII, éd. Ferret et McKenna, p. 183. « Il est faux que les petits soient moins agités que les grands ; au contraire, leurs désespoirs sont plus vifs parce qu'ils ont moins de ressources. De cent personnes qui se tuent à Londres, il y en a quatre-vingt-dix-neuf du bas peuple, et à peine une d'une condition relevée. La comparaison de la roue est ingénieuse et fausse. »
Voir la réponse, assez faible, de Boullier, Sentiments de M*** sur la critique des Pensées de Pascal par M. Voltaire, § XXXVIII, p. 190. « Comment peut-on soutenir, qu’il est faux que les petits soient moins agités que les grands par les mêmes passions ? De quelle foule d’autorités ne pourrait-on pas écraser cette critique, s’il s’agissait ici de cela ? Suffit que pour contredire Pascal, M. de V. contredit la raison, l’expérience et l’opinion générale des hommes. La comparaison de la roue qui agite davantage par son mouvement ceux qui sont au haut, que ceux qui demeurent près du centre, n’est donc pas seulement ingénieuse ; elle est pleine de vérité et de justesse ».
Montaigne, Essais, II, 12, éd. Balsamo et alii, Pléiade, p. 500. « Les âmes des empereurs et des savetiers sont jetées à même moule. Considérant l'importance des actions des princes et leur poids, nous nous persuadons qu'elles soient produites par quelques causes aussi poisantes et importantes. Nous nous trompons : ils sont menés et ramenés en leurs mouvements par les mêmes ressorts, que nous sommes aux nôtres. La même raison qui nous fait tanser avec un voisin, dresse entre les princes une guerre : la même raison qui nous fait fouetter un laquais, tombant en un roi, lui fait ruiner une province. Ils veulent aussi légèrement que nous, mais ils peuvent plus. Pareils appétits agitent un ciron et un éléphant. »
Mesnard Jean, Les Pensées de Pascal, 2e éd., 1993, p. 76. Exemple d’usage de l’imagination qui introduit une structure mathématique dans le domaine de la réflexion philosophique. Le passage de Montaigne dont Pascal s’inspire ne contient pas ce procédé de stylisation. Les arches de la roulette (cycloïde) figurent concrètement les « mouvements » qui agitent petits et grands.
L’image d’un cercle tournant autour de son centre suffit à illustrer cette maxime. Si plusieurs circonférences concentriques y sont inscrites, celles dont les points subissent la plus grande agitation sont celles dont le rayon est le plus grand. Le centre, lui, demeure immobile.
L’emploi du mot roue donne cependant à penser que Pascal fait allusion à la roulette (cycloïde), à laquelle il a consacré les Lettres de A. Dettonville. La roue (rota), dans le vocabulaire de Roberval et de Pascal, désigne le cercle qui se déplace. Le centre ne subit qu’un déplacement rectiligne, parallèle à la base. En revanche, un point placé sur la circonférence trace une courbe en arche.
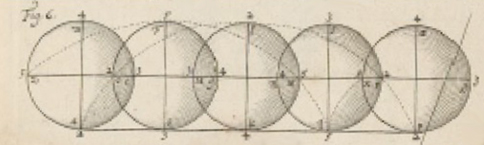
Dessin du P. Tacquet.
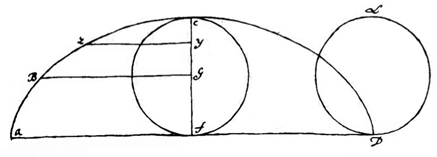
Dessin de Pascal.
On peut prendre le point traçant, non sur la circonférence du cercle porteur (rota), mais à l’intérieur ou à l’extérieur, ce qui engendre deux courbes différentes. Roberval, De trochoide, in Mémoires de l’Académie des sciences, VI, p. 295, distingue la trochoides rotae contractae, si circulus circa axem trochoidis descriptus major sit quam rota, c’est-à-dire si le point est pris en dehors du cercle générateur (rota) ; et trochoides rotae prolatae, si circulus minor sit ipsâ rotâ, donc si le point est à l’intérieur du cercle. Cette nomenclature se justifie si on considère non la courbe engendrée, mais le rapport du rayon de la roue et de celui qui porte le point traçant.
La roulette dont la roue est allongée (rotae prolatae) revêt l’aspect suivant. Le point traçant A, proche du centre O de la roue, suit une courbe moins tourmentée que dans le cas d’une roulette ordinaire.

La roulette dont la roue est accourcie (rotae contractae), où le point traçant A est à l’extérieur de la circonférence, au contraire, comporte non seulement une amplitude plus grande, mais aussi des points où elle se coupe elle-même.
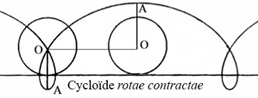
De nos jours, les adjectifs allongé et raccourci sont plutôt appliqués à la courbe de la roulette elle-même, et non plus à la roue, ce qui a entraîné une inversion des dénominations, de sorte que la trochoides rotae contractae de Roberval est appelée cycloïde allongée ou étendue, et la trochoides rotae prolatae devient la cycloïde raccourcie ou contractée. Le point qui trace la courbe est ici beaucoup plus « agité » que dans le cas précédent.
Les paradoxes que cette distinction soulève sont traités dans l’ouvrage du P. Tacquet André, Dissertatio physico-mathematica de motu circuli et sphaerae. Quam praeside R. P. Andrea Tacquet, Societatis Iesu matheseos professore defendit, explicuit ac demonstravit, Illustrissimus D. Philippus Eugenius comes de Hornes et d’Herlies, Lovanii 31 jan. Anno 1650, in Collegio Societatis Iesu, Lovanii, Typis Corn. Coenestenii, Anno 1650. Voir Descotes Dominique, “Documents relatifs aux Lettres de A. Dettonville, I, Pascal et le Père Tacquet”, Courrier du Centre International Blaise Pascal, 14, 1992, p. 18-53.
✍
Merker Claude, Le chant du cygne des indivisibles. Le calcul intégral dans la dernière œuvre scientifique de Pascal, Besançon, Presses Universitaires Franc-Comtoises, 2001.
Descotes Dominique, Blaise Pascal. Littérature et géométrie, 2001.
Carraud Vincent, Pascal. Des connaissances naturelles à l’étude de l’homme, Paris, Vrin, 2007, p. 219 sur ce fragment.

