Rechercher :

    

Fragment Transition n° 4 / 8  – Papier original : RO 347 r/v°, 351 r/v°, 355 r/v°, 359 r/v°

Copies manuscrites du XVII^e s. : C₁ : Transition n° 248 à 257 p. 91 à 99 v° / C₂ : p. 117 à 129

Éditions de Port-Royal :

    Chap. XXII - Connoissance générale de l’homme : 1669 et janv. 1670 p. 171-178 / 1678 p. 168-174 (chap. complet)

    Chap. XXXI - Pensées diverses : 1669 et janv. 1670 p. 331-335 / 1678 n° 27 p. 326-330

Éditions savantes : Faugère II, 63, I ; II, 68, II ; II, 75, II / Havet I.1 / Brunschvicg 72 / Tourneur p. 236-1 / Le Guern 185 / Maeda I p. 219 / Lafuma 199 / Sellier 230

______________________________________________________________________________________

 

 

✧ Éclaircissements

 

 

 

Que l’homme étant revenu à soi considère ce qu’il est au prix de ce qui est, qu’il se regarde comme égaré dans ce canton détourné de la nature. Et que, de ce petit cachot où il se trouve logé, j’entends l’univers, il apprenne à estimer la terre, les royaumes, les villes et soi‑même, son juste prix.

 

Étant revenu à soi : au sens propre, remarque Havet, étant revenu à se considérer lui-même.

Contrariétés 1 (Laf. 119, Sel. 151). Contrariétés. Après avoir montré la bassesse et la grandeur de l’homme. Que l’homme maintenant s’estime son prix.

Cette phrase marque le début du second temps, avec un mouvement inverse de diminution à l’infini.

De Gandillac Maurice, “Pascal et le silence du monde”, in Blaise Pascal. L’homme et l’œuvre, Colloque de Royaumont, Paris, Éditions de Minuit, 1956, p. 342-365, suivi d’une discussion, p. 366-385. Voir p. 348 sq. ✍

De l’Esprit géométrique, § 39-40, OC III, p. 411-412. « Ceux qui ne seront pas satisfaits de ces raisons, et qui demeureront dans la créance que l’espace n’est pas divisible à l’infini, ne peuvent rien prétendre aux démonstrations géométriques ; et, quoi qu’ils puissent être éclairés en d’autres choses, ils le seront fort peu en celles ci : car on peut aisément être très habile homme et mauvais géomètre. Mais ceux qui verront clairement ces vérités pourront admirer la grandeur et la puissance de la nature dans cette double infinité qui nous environne de toutes parts, et apprendre par cette considération merveilleuse à se connaître eux-mêmes, en se regardant placez entre une infinité et un néant d’étendue, entre une infinité et un néant de nombre, entre une infinité et un néant de mouvement, entre une infinité et un néant de temps. Sur quoi on peut apprendre à s’estimer son juste prix, et former des réflexions qui valent mieux que tout le reste de la géométrie. J’ai cru être obligé de faire cette longue considération en faveur de ceux qui, ne comprenant pas d’abord cette double infinité, sont capables d’en être persuadés. Et, quoi qu’il y en ait plusieurs qui aient assez de lumière pour s’en passer, il peut néanmoins arriver que ce discours, qui sera nécessaire aux uns, ne sera pas entièrement inutile aux autres. »

Susini Laurent, L’écriture de Pascal. La lumière et le feu. La « vraie éloquence », à l’œuvre dans les Pensées, p. 571. Sur l’image du cachot. ✍

 

Qu’est‑ce qu’un homme, dans l’infini ?

 

Maeda Yoichi, Commentaire…, p. 209. Première version : « qu’est-ce qu’un homme dans la Nature ? »

 

Mais pour lui présenter un autre prodige aussi étonnant,

 

♦  La relativité des deux infinis 

 

L’idée de la relativité des deux infinités remonte à l’Antiquité : voir Aristote, Physique, III, 206, éd. Couloubaritsis, p. 144 sq. « L’infini par addition est d’une certaine manière le même que celui par division ; en effet, dans la chose finie, l’infini par addition advient inversement, car, dans la mesure où l’on voit la chose divisée à l’infini, augmentée d’autant, elle apparaît aller vers le défini. En effet, dans la grandeur finie, si, après avoir pris une partie définie, on en prend en outre suivant la même proportion [c’est-à-dire en divisant cette partie d’autant que la première : si on a commencé par la moitié, on prendra ensuite la moitié de la moitié], sans circonscrire une grandeur identique au tout on ne parcourra pas le fini ; mais si l’on augmente la proportion de manière à circonscrire toujours la même grandeur, on la parcourra, du fait que toute chose finie est épuisée par n’importe quelle partie définie. » Voir le commentaire de Heath Thomas, Mathematics in Aristotle, p. 105 sq.

Euclidis Elementorum libri XV, […] auctore Christophoro Clavio bambergensi, e societate Jesu, p. 13. « Item quacunque magnitudine data, sumi posse aliam magnitudinem vel majorem, vel minorem ». « Omnis enim quantitas continua per additionem augeri, per divisionem vero diminui potest infinite : unde nunquam dabitur quantitas continua adeo magna, quin ea major dari possit ; neque tam parva, quin minor ea possit exhiberi. Hoc idem in numeris verum est, quoad ad additionem pertinet. Nam quilibet numerus per continuam additionem unitattis augeri potest infinite : quamvis in ejus diminutione ad unitate individuam deveniatur. »

L’idée de la jonction de la connaissance de l’infiniment grand et de l’infiniment petit, se retrouve encore chez Galilée, Discours concernant deux sciences nouvelles, éd. M. Clavelin, Paris, Colin, 1970, p. 29 sq., qui prétend « appréhender ensemble l’infini et l’indivisible ».

Dans le milieu que Pascal fréquente, c’est une idée fondamentale dans la géométrie arguésienne : voir Desargues Girard, Brouillon projet, éd. Taton, in L’œuvre mathématique de Girard Desargues, p. 115, sur l’homologie, dans une involution, entre la souche et le point à l’infini ; ils déterminent des branches extrêmes, dont « la petite est apetissée jusqu’à la souche, et la grande est allongée à l’infini » ; éd. Poudra, I, p. 248-249.

Cette idée est présente dans De l’Esprit géométrique, OC III, éd. J. Mesnard, p. 410 sq. (1655). Voici le texte :

§ 36. « Voilà l’admirable rapport que la nature a mis entre ces choses, et les deux merveilleuses infinités qu’elle a proposées aux hommes, non pas à concevoir, mais à admirer ; et pour en finir la considération par une dernière remarque, j’ajouterai que ces deux infinis, quoique infiniment différents, sont néanmoins relatifs l’un à l’autre, de telle sorte que la connaissance de l’un mène nécessairement à la connaissance de l’autre.

37. Car dans les nombres, de ce qu’ils peuvent toujours être augmentés, il s’ensuit absolument qu’ils peuvent toujours être diminués, et cela clairement : car si l’on peut multiplier un nombre jusqu’à 100 000, par exemple, on peut aussi en prendre une 100 000^e partie, en le divisant par le même nombre qu’on le multiplie, et ainsi tout terme d’augmentation deviendra terme de division, en changeant l’entier en fraction. De sorte que l’augmentation infinie enferme nécessairement aussi la division infinie.

38. Et dans l’espace le même rapport se voit entre ces deux infinis contraires ; c’est à dire que, de ce qu’un espace peut être infiniment prolongé, il s’ensuit qu’il peut être infiniment diminué, comme il paraît en cet exemple : Si on regarde au travers d’un verre un vaisseau qui s’éloigne toujours directement, il est clair que le lieu du diaphane, où l’on remarque un point tel qu’on voudra du navire, haussera toujours par un flux continuel à mesure que le vaisseau fuit. Donc, si la course du vaisseau est toujours allongée et jusques à l’infini, ce point haussera continuellement ; et cependant il n’arrivera jamais à celui où tombera le rayon horizontal mené de l’œil au verre, de sorte qu’il en approchera toujours sans y arriver jamais, divisant sans cesse l’espace qui restera sous ce point horizontal, sans y arriver jamais. D’où l’on voit la conséquence nécessaire qui se tire de l’infinité de l’étendue du cours du vaisseau, à la division infinie et infiniment petite de ce petit espace restant au-dessous de ce point horizontal.

39. Ceux qui ne seront pas satisfaits de ces raisons, et qui demeureront dans la créance que l’espace n’est pas divisible à l’infini, ne peuvent rien prétendre aux démonstrations géométriques ; et, quoi qu’ils puissent être éclairés en d’autres choses, ils le seront fort peu en celles-ci : car on peut aisément être très habile homme et mauvais géomètre.

Mais ceux qui verront clairement ces vérités pourront admirer la grandeur et la puissance de la nature dans cette double infinité qui nous environne de toutes parts, et apprendre par cette considération merveilleuse à se connaître eux-mêmes, en se regardant placés entre une infinité et un néant d’étendue, entre une infinité et un néant de nombre, entre une infinité et un néant de mouvement, entre une infinité et un néant de temps. Sur quoi on peut apprendre à s’estimer son juste prix, et former des réflexions qui valent mieux que tout le reste de la géométrie.

40. J’ai cru être obligé de faire cette longue considération en faveur de ceux qui, ne comprenant pas d’abord cette double infinité, sont capables d’en être persuadés. Et, quoi qu’il y en ait plusieurs qui aient assez de lumière pour s’en passer, il peut néanmoins arriver que ce discours, qui sera nécessaire aux uns, ne sera pas entièrement inutile aux autres. »

 

 

Arnauld Antoine et Nicole Pierre, La logique ou l’art de penser, IV, 1, p. éd. D. Descotes, Paris, Champion, 2011, p. 518 sq. Exemple de la division à l’infini, d’une mer plate et d’un vaisseau qui s’éloigne du port en ligne droite. La Logique souligne que cela montre la division à l’infini et en même temps d’un ralentissement, à l’infini du mouvement. L’idée de la corrélation des deux infinis manque pourtant dans ce passage.

Voir une construction équivalente dans Benedetti Giambattista, Diversarum speculationum liber, Disputationes de quibusdam placitis Aristotelis, cap. XXIX, Dari continuum infinitum motum super rectam atque finitam lineam. La construction de Benedetti est la suivante : « Omnes hactenus senserunt impossibile esse dati per imaginationem motum continuum et perpetuum super unam lineam rectam finitam quamdam decipiuntur. Imaginemur jam duas lineas parallelas ab et tx quarum ba sit infinita a qualibet parte, et in ea imaginemus punctum a moveri continuo ad quam voluerimus partem, et in linea tx imaginemur punctum fixum, quod sit c. Imaginemur etiam inter c et a unam lineam rectam ca et inter duas parallelas dictas, rx fixam, et motus puncti fit ab b versus a ita ut ca secet tx in puncto i quod intersectionis punctum monebitur ab. r versus x continuo, in tempore infinito, neque unquam idem erit cum puncto x ».

 

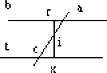
Robinet André, Malebranche de l’Académie des sciences, p. 74, trouve une construction analogue chez Malebranche, inspirée de Rohault, Traité de physique, I, IX, § IV, p. 48-49.

Couturat, De l’infini mathématique, p. 219 sq. M se déplace sur AX à vitesse constante. La longueur AM croît proportionnellement au temps. Elle sera toujours finie au bout d’un temps fini. La longueur AM devient infiniment grande, mais comme elle est toujours finie, on trouvera toujours dans l’ensemble des nombres réels finis un nombre correspondant à la position de M. Le point P qui coïncidait d’abord avec A, parcourt la circonférence de A en B : l’arc AP croît en même temps que AM. Il reste fini et inférieur à l’arc AB, qui correspond à l’angle droit AOB. Puisque OZ rencontre toujours AX à distance finie de A, elle ne peut venir coïncider avec OB, parallèle à AX. Donc P approche indéfiniment de B, de même que OZ approche indéfiniment de OB. L’arc BP décroît indéfiniment sans jamais s’annuler. Si on suppose que P se déplace d’un mouvement uniforme sur la circonférence de A vers B, si petite que soit sa vitesse, P arrivera en B en un temps fini. Où est M quand P est en B ? L’arc AP devient égal à sa limite AB. Donc AM prend sa valeur limite qui est l’infini. AX et OZ se rencontrent à l’infini. Ce raisonnement montre que deux droites dans un même plan ont toujours un point commun à distance infinie, sans que cela contredise l’axiome des parallèles : p. 222 sq.

 

 

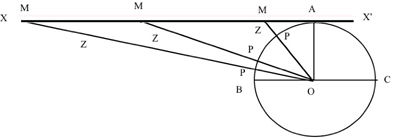
L’idée de la corrélation des deux infinis n’est pas acceptée par tous les savants. Voir Heath Thomas, Mathematics in Aristotle, p. 102 sq. La grandeur continue est divisible ad infinitum, mais dans le sens de l’accroissement il n’y a pas d’infini. Si c’était le cas, il y aurait quelque chose de plus grand que l’univers.

Voir les remarques critiques de Gardies Jean-Louis, Pascal entre Eudoxe et Cantor, p. 69.

 

qu’il recherche dans ce qu’il connaît les choses les plus délicates, qu’un ciron lui offre dans la petitesse de son corps des parties incomparablement plus petites, des jambes avec des jointures, des veines dans ses jambes, du sang dans ses veines, des humeurs dans ce sang, des gouttes dans ses humeurs, des vapeurs dans ces gouttes ; que divisant encore ces dernières choses, il épuise ses forces en ces conceptions, et que le dernier objet où il peut arriver soit maintenant celui de notre discours. Il pensera peut‑être que c’est là l’extrême petitesse de la nature.

 

Pascal n’utilise pas l’infiniment petit de la même manière que les apologistes de son temps. Voir Jovy Ernest, “Les antécédents de l’infiniment petit”, in Études pascaliennes, VIII, p. 9-103 ; Vrin-Reprise, p. 123-218. Ce que les auteurs trouvent admirable, c’est la composition remarquable des organismes microscopiques : on admire l’ordre de la nature dans l’infiniment petit. Voir p. 131, sur saint Augustin, Enarr. in Ps. 150. On remarque aussi la disproportion entre la petitesse de l’organisme et sa vigueur, le tout à la louange du « grand géomètre » qui l’a créé. Voir aussi Du Vair, De la sainte Philosophie, éd. Michaux, Paris, Vrin, 1946, p. 52-53, pour le style, dans une décomposition de l’organisme, qui vise à montrer l’ordre, et non l’infinie divisibilité. « Que l’homme s’arrête un peu en soi-même ; qu’il cherche seulement quel il est, comment un peu d’humeur s’accroît et s’augmente de telle façon qu’il s’en forme un corps, composé en tant de diverses parties, avec telle proportion. Mais qu’il ne se contente pas de se voir droit sur ses pieds, ayant la face élevée, les yeux ouverts et remuant tous ses membres. Qu’il découvre un peu la peau ; qu’il devine comment sa chair et ses os sont si artificieusement assemblés ; qu’il remarque comme tant de nerfs et de muscles sont tirés depuis le  cerveau jusques aux plus petites extrémités du corps pour bander, lâcher, et remuer toutes les parties à toutes sortes de mouvements ; qu’il regarde comment tant de veines sont répandues par tout le corps, pour porter le sang et la nourriture à chacun des membres ; qu’il voie comment tant d’artères sont conduites du cœur et départies pour accompagner tous les nerfs et les veines, pour conduire en chaque partie les esprits, comme messagers de sa volonté, afin de donner commandement au nerf de se mouvoir ou arrêter… » Du Vair poursuit dans le même style, dont le rythme n’est pas très éloigné de celui de Pascal.

On retrouve le même éloge des merveilles de l’infiniment petit  chez Fénelon, Traité de l’existence de Dieu, I, II, § 21, éd. Dumas, p. 31 sq.

Mais Pascal porte l’accent non pas sur l’ordre cosmique, mais sur la division de la matière, qui peut se poursuivre sans fin, jusqu’à donner le vertige.

Wallis John, De cycloide, p. 534. Magnitudines in infinitum descrescente sunt quarum non datur minima.

Meurillon Christian, “Clés pour le lexique des Pensées : L’exemple de corps”, in L’Accès aux Pensées de Pascal, p. 125-143. ✍

McKenna Antony, “Pascal et le corps humain”, in Pascal, XVII^e siècle, 177, octobre-décembre 1992, p. 481-494. ✍

 

♦  Le ciron

 

Sur les petits animaux chez les apologistes, voir Julien-Eymard d’Angers, Pascal et ses précurseurs, p. 139 sq. Poissons, vers à soie, moucherons, fourmis. Ils décrivent les animalcules organe par organe, en soulignant leur coexistence. Il n’y a pas de subdivision indéfinie chez les précurseurs de Pascal. Voir Yves de Paris, Théologie naturelle (1645) III, p. 215-216 (éd. de 1635 : p. 228-229).

C’est un exemple classique : voir Lenoble Robert, Mersenne, p. 250 sq. Le ciron revient en effet un peu partout chez Mersenne.

Mersenne Marin, Quaestiones in Genesim, col. 127-128.

Mersenne Marin, Correspondance, II, p. 201.

Mersenne Marin, La vérité des sciences, IV, ch. I, éd. D. Descotes, Paris, Champion, 2003, p. 725. Problème de l’infinité d’infinités de parties dans une ligne ou un corps : « il y aurait dans chaque corps plus petit un million de fois qu’un ciron, une infinité de corps infinis en parties, dans la surface desquels il y aurait plusieurs infinités de plans infinis et autant d’infinités d’indivisibles, ce qui semble fort étrange, et contre toute sorte de vérité », p. 726. Voir p. 728 : « L’unité contient toutes sortes de nombres, lesquels se résolvent tous en icelle, mais la quantité ne se peut résoudre en un point, quant à ce qui est de ses parties internes, et essentielles : car pour les externes, ou l’extension, par laquelle elle se rend visible, et palpable et occupe un certain lieu, Dieu l’en peut dépouiller, comme d’une propriété, sans laquelle elle peut subsister par vertu divine, par laquelle tout le firmament pourrait être renfermé dans l’extrémité du pied d’un ciron, tant petit soit-il. »

Le ciron a fait l’objet de grands calculs chez le P. Mersenne. Voir Questions inouïes, Q.VII, éd. Pessel, p. 25 sq. « Et si l’homme est plus grand au regard de la terre, qu’un ciron au regard de l’homme ». On suppose le ciron gros comme deux grains de sable ; il faudrait 120 932 352 000 cirons pour faire un homme. Le rapport de l’homme à la Terre est 58 587 771 655 fois plus grand que le rapport de l’homme au ciron. « D’où chacun peut conclure quelle estime l’on doit faire de l’homme, et qu’il est bien aisé de dompter son ambition » (p. 26). Noter que Mersenne fournit la cubature du ciron, qu’il évalue à deux grains de sable ; ce qui lui permet de calculer combien de cirons contiendrait un bateau.

L’idée que l’on peut retrouver des cirons analogues aux premiers au terme d’une division indéfinie se trouve déjà chez Mersenne : voir Mersenne, Harmonie universelle, Livre III, Prop. XIV, éd. C.N.R.S., t. 1, p. 188. Supputations harmoniques sur le ciron, et sur une corde aussi déliée que sa patte. « Et l’on ne sait pas s’il n’y a point encore d’autres animaux dans le ciron, qui soient aussi petits à son égard, comme il est au nôtre : ce qui doit empêcher la précipitation du jugement de ceux qui croient que tout ce qu’ils ne voient pas, ou ce qu’ils ne peuvent apercevoir n’est pas, ou ne peut être ». Mais Mersenne n’en tire pas les mêmes effets de vertige que Pascal.

Cyrano de Bergerac, États et empires de la lune, Œuvres complètes, Belin, 1977, p. 405, parle de la cironalité universelle : p. 406 ; ou Les états et empires de la lune et du soleil, éd. M. Alcover, Paris, Champion, 2004, p. 116 sq.

Noter que la carrière de la bestiole ne s’arrête pas là : on la retrouve chez Fénelon, Traité de l’existence de Dieu, I, II, § 21 ; chez La Bruyère, Caractères, VII, 44 ; et même chez Sartre Jean-Paul, Les Mouches, III, 2, éd. N.R.F., p. 110.

 

Je veux lui faire voir là‑dedans un abîme nouveau. Je lui veux peindre non seulement l’univers visible, mais l’immensité qu’on peut concevoir de la nature dans l’enceinte de ce raccourci d’atome ;

 

Ce raccourci d’atome : sur cet oxymore associé à un adynaton (puisque par définition on ne peut raccourcir un atome), voir OC III, éd. J. Mesnard, p. 353 sq., les réflexions de Méré sur ce point. ✍

L’imagination prend ici le relais à partir du visible, comme cela a été le cas pour l’infini de grandeur, avec un style plus impérieux que plus haut. Voir Lanavère Alain, “L’argument des deux infinis…”, p. 85. Sur le vertige ainsi engendré par le rythme que Pascal impose à son texte, voir la belle analyse proposée p. 89 sq.

Second temps de l’argument sur l’infiniment petit. L’opération de division n’est plus mentionnée ; elle est sous-entendue à cause du mouvement précédent, et automatiquement réitérée. Mais la transition de la perception à l’imagination, en passant par « l’extrême petitesse de la nature » garantit que toutes les grandeurs auxquelles on aura affaire désormais pourront être comptées comme des néants à l’égard des précédentes, ou, pour parler comme les mathématiciens contemporains de Pascal, comme plus petits que toute grandeurs donnée à volonté.

Pascal s’inspire ici de la démarche qu’il met en œuvre dans les Lettres de A. Dettonville, notamment dans le Traité des trilignes, OC IV, éd. J. Mesnard, p. 465. Pour montrer que certaines petites surfaces, même si on les prend toutes, demeurent négligeables par rapport à une grandeur donnée, Pascal envisage un rectangle de côtés X et Y. Il divise le côté X en petites subdivisions égales x, sur lesquelles il construit des petits rectangles de côté x et de longueur égale chacune à des lignes aux ordonnées d’une figure donnée (en bleu sur la figure). La construction lui permet d’affirmer que la somme des petits rectangles bleus forme une surface qui sera toujours inférieure au rectangle initial. Si petit que l’on suppose ce rectangle, a fortiori la somme des rectangles bleus sera moindre ; et par conséquent si on le suppose moindre que toute grandeur donnée, a fortiori la somme des rectangles bleus sera plus petite encore, c’est-à-dire négligeable. Sur ce raisonnement, voir Descotes Dominique, Blaise Pascal. Littérature et géométrie, Clermont-Ferrand, Presses Universitaires Blaise Pascal, 2001, p. 218 sq., et Merker Claude, Le chant du cygne des indivisibles, Presses Universitaires Franc-Comtoises, p. 123 sq.

 

 

 

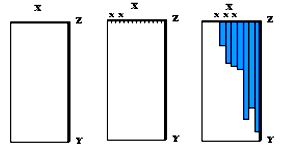
Le postulat de cette argumentation est que la division indéfinie ne change pas la nature de l’objet. C’est un problème envisagé par les scolastiques comme problème du minimum naturel d’une substance : la division à l’infini ne modifie-t-elle pas la substance de ce sur quoi elle porte ? Voir Duhem Pierre, Le système du monde, VII, p. 42 ; Aristote, Physique, I, IV : le volume de la chair, par exemple, est borné en grandeur et en petitesse, car on ne peut pas la découper indéfiniment sans la détruire. Voir ibid., p. 44 : le même principe énoncé par saint Thomas.

Susini Laurent, L’écriture de Pascal. La lumière et le feu. La « vraie éloquence », à l’œuvre dans les Pensées, p. 441 sq. Technique du style coupé dans ce passage. Voir aussi p. 576, sur la technique de substitution de la profondeur à l’idée de la division.

© Crédits et Mentions légales