Pensées de Blaise Pascal

Rechercher :

Pensées diverses I – Fragment n° 12 / 37 – Papier original : RO 110-2

Copies manuscrites du XVII^e s. : C₁ : n° 93 p. 335-335 v° / C₂ : p. 287-287 v°

Un § a été ajouté dans l’édition de 1678 : Chap. XXXI - Pensées diverses : 1678 n° 36 p. 333

Éditions savantes : Faugère I, 255, XXVII ; I, 189, XXXIII ; I, 257, XXX / Havet VII.23 et XXV.63 / Brunschvicg 45 et 114 / Tourneur p. 76-4 / Le Guern 479 / Lafuma 557 et 558 (série XXIII) / Sellier 465

______________________________________________________________________________________

Bibliographie ✍

BÉLY Lucien, Espions et ambassadeurs au temps de Louis XIV, Paris, Fayard, 1990.

FORCE Pierre, Le problème herméneutique chez Pascal, Paris, Vrin, 1989.

IFRAH Georges, Histoire universelle des chiffres, Paris, Bouquins, R. Laffont, 1994, 2 vol.

L’art de déchiffrer, Traité de déchiffrement du XVII^e siècle de la secrétairerie d’État et de guerre espagnole, éd. J. P. Devos et H. Seligman, Publications universitaires de Louvain, 1967.

MAGNARD Pierre, Le vocabulaire de Pascal, Paris, Ellipses, 2001.

MARIN Louis, La critique du discours, Paris, éd. de Minuit, 1975, p. 115 sq.

MARIN Louis, “Une ville, une campagne, de loin... : paysages pascaliens”, Littérature, 61, fév. 1986, p. 3-16 ; repris in Pascal et Port-Royal, éd. A. Cantillon et alii, Paris, P. U. F., 1997, p. 196-213.

MESNARD Jean, Les Pensées de Pascal, 2^e éd., Paris, SEDES-CDU, 1993.

MESNARD Jean, “Desargues et Pascal”, in Desargues en son temps, éd. Dhombres J. et J. Sakarovitch, Blanchard, Paris, 1994, p. 87-99.

MESNARD Jean, “Point de vue et perspective dans les Pensées”, Courrier du Centre International Blaise Pascal, 16, Clermont-Ferrand, 1994, p. 3 sq. , repris dans Treize études sur Blaise Pascal, Clermont, P. U. Blaise Pascal, 2004,p. 11-24.

MULLER André, Les écritures secrètes, Que sais-je ?, Paris, P. U. F., 1971.

SERRES Le Système de Leibniz et ses Modèles mathématiques, t. 2, Paris, P. U. F., Paris, 1968.

WRIXON Fred, Langages secrets. Codes, chiffres et autres cryptosystèmes, Cologne, Könemann, 2000.

Voir plus bas la bibliographie relative à Girard Desargues.

✧ Éclaircissements

Les langues sont des chiffres, où non les lettres sont changées en lettres, mais les mots en mots.

Pascal entend par chiffre un système de substitution des lettres selon un système fixé. Les langues entrent sous la catégorie générale des chiffres, c’est-à-dire que d’une langue à l’autre, ce sont les mots qui changent.

Magnard Pierre, Le vocabulaire de Pascal, p. 6 sq. Le mot chiffre désigne une écriture secrète utilisée par les chancelleries pour assurer la confidentialité des messages, par les savants pour préserver la propriété de leurs inventions.

Chiffre est aussi un caractère mystérieux composé de quelques lettres entrelacées ensemble qui sont d’ordinaire les lettres initiales du nom de la personne pour qui il est fait. Chiffre se dit de certains caractères inconnus déguisés et variés, dont on se sert pour écrire des lettres, qui contiennent quelques secrets, et qui ne peuvent être entendus que par ceux qui sont d’intelligence, et qui sont convenus ensemble de se servir de ces caractères. On en a fait une science qu’on appelle Polygraphie, ou Stéganographie, c’est-à-dire écriture diversifiée et obscure, laquelle a été inconnue aux anciens. Trithème et depuis Jean-Baptiste Porta en ont écrit fort savamment. Vigenère et le Père Niceron en ont aussi écrit (Furetière).

Force Pierre, Le problème herméneutique..., p. 100 sq. Voir, sur l'idée du chiffre, les fragments Loi figurative 20 (Laf. 265, Sel. 296) et Loi figurative 31 (Laf. 276, Sel. 307).

Ifrah Georges, Histoire universelle des chiffres, II, coll. Bouquins, p. 371 sq. Sens de chiffrer : marquer une correspondance secrète.

Parmi les auteurs qui ont traité des chiffres, figurent Porta Giovanni, De furtivis literarum notis, 1563 ; Cardan, De secretis, De subtilitate, De rerum varietate, in Opera omnia, 10 vol., Lyon, J. A. Huguetan et M. A. Ravaud, 1663 ; Vigenère Blaise de, Traité des chiffres, Paris, chez Abel L’Angelier, 1586.

Viète a été un spécialiste reconnu du déchiffrement des codes secrets. Voir Viète François, Deschiffrement d’une lettre escripte par le Commandeur Moreo au Roy d’Espagne son maître, du 28 octobre 1589, Tours, Mettayer, 1590. Tallemant des Réaux, Historiettes, I, éd. Adam, Pléiade, 1960, p. 871, s’est fait l’écho de son talent comme spécialiste du déchiffrement.

La théorie cryptographique du chiffre, telle qu’elle est conçue à l’époque classique, est exposée avec précision dans L’art de déchiffrer, Traité de déchiffrement du XVII^e siècle de la secrétairerie d’État et de guerre espagnole, éd. J. P. Devos et H. Seligman. « Le chiffre n’est autre chose, pour parler en termes de l’École, qu’une troisième signification médiate des pensées des hommes, réglées et concertée entre deux ou plusieurs personnes pour se faire connaître leurs sentiments par écrit et les déguiser à tous ceux qui ne sont pas du ministère ». Troisième signification, « parce que le premier signe de la pensée de l’homme est la parole par laquelle nous expliquons aux autres ce qui n’est connu qu’à nous-mêmes » : p. 5. « Le second est l’écriture qui est un signe de la parole et par conséquent un signe médiat de la pensée et le troisième est le chiffre qui est un signe immédiat de l’écriture, et partant un second signe de la parole et un troisième signe de la pensée » : p. 5.

Selon GEF XII, p. 52, l’expression les lettres changées en lettres fait allusion aux systèmes moitié sténographiques, moitié cryptographiques qui avaient été proposés surtout en Angleterre. Sur les cryptographes anglais, voir Wrixon Fred, Langages secrets, p. 30 sq. Les guerres civiles en Angleterre ont suscité des vocations de cryptanalystes, parmi lesquels on peut nommer Thomas Phelippes, p. 31 ; et John Wallis, considéré comme le père de la cryptographie anglaise : p. 34. La France compte aussi de célèbres crypteurs. Voir sur ce sujet Bély Lucien, Dictionnaire Louis XIV, Paris, Robert Laffont, 2015, p. 294-297, et Bély Lucien, Espions et ambassadeurs au temps de Louis XIV, Paris, Fayard, 1990, p. 154-157. Le cryptanalyste le plus célèbre est Antoine Rossignol : p. 35. Voir aussi sur lui Bély Lucien, Dictionnaire Louis XIV, Paris, Robert Laffont, 2015, p. 295-296.

Mais le chiffre secret n’est qu’un cas d’une réalité plus large. La substitution d’une lettre à une autre n’a pas nécessairement pour but la dissimulation. Elle peut aussi tendre au contraire à faire découvrir la vérité. Les contemporains de Pascal, lorsqu’ils parlent de chiffre, n’ont pas nécessairement en tête le langage des correspondances secrètes, mais aussi les systèmes symboliques tels que les écritures algébriques. Chiffre désigne d’abord le caractère qui sert à exprimer un nombre. D’autre part, Descartes désigne l’écriture algébrique de sa Géométrie comme un chiffre, destiné à remplacer les systèmes dits cossiques, qui sont aujourd’hui oubliés. Voir Descartes, Géométrie, Livre I, Comment on peut user de chiffres en géométrie, AT VI, p. 371. Sur ce remplacement des signes cossiques par une écriture algébrique simplifiée, voir le Discours de la méthode, éd. Gilson, 6^e éd., Paris, Vrin, 1987, p. 221 ; Costabel Pierre, “Les Essais de la Méthode...”, in Le Discours et sa méthode, P. U. F., Paris, 1987, p. 220, et Costabel Pierre, Démarches originales de Descartes savant, Vrin, Paris, 1982, p. 5 et 187. L’algèbre permet à Descartes de chiffrer la géométrie par l’arithmétique dans une langue artificielle et d’y transposer les problèmes. Comme tout chiffre, l’algèbre de Descartes comporte une opération de codage, et une opération de décodage. L’algèbre permet de chiffrer la géométrie classique par l’arithmétique dans une langue artificielle, et d’en transposer les problèmes dans une langue artificielle dont il s’agit ensuite, après des transformations plus ou moins complexes des équations, de décoder les produits.

Pascal a usé d’un système de chiffre dans ses propres écrits mathématiques, quoique d’une manière différente de Descartes. On en trouve un exemple significatif dans la manière dont il désigne les cellules du Triangle arithmétique non par les nombres qu’elles contiennent, mais par des lettres (OC II, éd. J. Mesnard, p. 1176 sq. (version en latin) et p. 1288 sq. (version en latin). Dans l’article “Traité du triangle arithmétique, etc. : vue d’ensemble”, in L’œuvre mathématique de Pascal, Memoirs of the Faculty of Letters, Osaka University, vol. XXI, mars 1981, p. 37-38, Kokiti Hara note qu’on y constate l’apparition d’une « arithmétique symbolique ». Voir aussi la manière dont Pascal procède dans le De numeris multiplicibus ex sola characterum numericorum additione agnoscendis, OC II, éd. J. Mesnard, p. 1272 sq.

Pascal a approfondi le problème technique des chiffres de la manière la plus pratique. On sait que les dessins de la page 20 du Recueil des originaux (au verso du fragment RO 19-1 (Laf. 818-820, Sel. 660)) ont été interprétés comme un système de chiffre, demeuré à ce jour mystérieux. On devine seulement que les différentes « notes » représentent des caractères (lettres, notes de musique ou autre) et que la ligne qui se trouve en haut à droite du papier représente une phrase, un air de musique ou une séquence de caractères non identifiés.

Lorsqu’il écrit que les lettres sont changées en lettres, Pascal n’entend pas nécessairement que chaque lettre chiffrante est toujours transformée en une seule et même lettre chiffrée. Bien au contraire, une bonne part de l’efficacité des chiffres à secret repose sur le fait qu’ils tendent à briser l’univocité qui peut exister entre les lettres. On attribue généralement à Pascal l’invention d’un alphabet artificiel : OC III, éd. J. Mesnard, p. 1612 sq. Origine : Bibliothèque du musée Calvet d’Avignon, ms. 1030. « L’art de déchiffrer les écritures en chiffres n’est point le résultat des coups du hasard ; ce n’est point une divination. Il faudrait être maître sorcier pour déchiffrer l’écriture artificielle ; et comme on sait, ce n’est pas être sorcier que de croire aux sorciers » : OC III, éd. J. Mesnard, p. 1617. Cet alphabet artificiel repose précisément sur un procédé qui permet de faire correspondre à une lettre chiffrante donnée une grande variété de lettres chiffrées, de sorte qu’il supprime entièrement toute relation univoque et constante entre les unes et les autres. Ce système repose sur une application habile de la théorie des combinaisons et sur l’usage d’une phrase clé (la phrase du guet). Le code est quasi incassable, parce qu’il est fondé sur des substitutions de lettres, selon une règle qui varie en fonction de cette phrase clé inconnue, qui peut être changée à volonté.

La substitution peut aussi s’effectuer de mot à mot, ce qui permet de construire des codes secrets pittoresques. Les correspondances du milieu janséniste témoignent que le recours aux chiffres pour échapper aux contrôles policiers y est devenu très fréquent. Pascal a eu entre les mains l’ouvrage du jésuite Pinthereau intitulé La naissance du jansénisme découverte à Monseigneur le Chancelier par le sieur de Préville, Louvain, Veuve Jacques Gravius, 1654, qui ouvre l’édition de la correspondance entre Jansénius et Saint-Cyran par une table de correspondance qui dévoile le code secret établi entre les deux personnages. On y constate que l’Augustinus est désigné par le mot de code Pilmot, que Jansénius est selon les cas Quinquarbre, Sulpice ou Cudaro, et que Saint-Cyran s’appelle Rongeart ou Durillon. Louis XIII aurait sans doute été surpris d’apprendre qu’il y était désigné sous le nom de Panar.

L’usage d’un tel chiffre peut avoir des applications inattendues. Voir OC IV, éd. J. Mesnard, p. 243. Pascal s’en sert dans certaines contestations scientifiques. Pour dénouer le conflit qui l’oppose au jésuite Lalouvère, Pascal lui propose de donner sa solution en langage chiffré à une personne de confiance, pour que l’on puisse la comparer à celle que Pascal entend lui-même publier dans ses Lettres de A. Dettonville. Lorsque chacun des deux rivaux aura communiqué ses solutions sous forme chiffrée, Pascal propose de les décrypter en même temps, et de les comparer pour voir laquelle est exacte. Il indique que, lorsqu'il propose à Lalouvère de donner sa solution en chiffre, son chiffre à lui est déjà fait.

Cependant la réflexion de Pascal porte dans ce fragment moins sur le chiffre que sur la nature des langues. Les langues entrent sous la catégorie générale des chiffres : d’une langue à l’autre, ce sont les mots qui changent.

Pascal ne dit pas que la correspondance des mots est de un à un, mais en général qu’il existe des correspondances entre mots. Il n’exclut donc pas la mise en correspondance entre un mot d’une langue et plusieurs mots d’une autre, comme dans le cas où sum traduit je suis.

D’autre part, les pages de la Logique ou l’art de penser relatives aux significations accessoires montrent que les Messieurs de Port-Royal étaient très conscients que, d’une langue à l’autre, les connotations attachées aux mots devaient nécessairement différer.

L’analogie entre le décryptage par équivalence de lettres et par équivalence de mots a été discutée : voir sur ce point Pensées, éd. Havet, I, Delagrave, 1866, p. 110.

Certains chiffreurs tentent de tourner la définition que Pascal donne dans ce fragment. Voir par exemple la méthode de chiffrement d’Antoine Rossignol selon Bély Lucien, Dictionnaire Louis XIV, Paris, Robert Laffont, 2015, p. 295-296 : son système de chiffrement vise à rendre la traduction ou le déchiffrement difficile parce qu’elle ne respecte pas l’homogénéité des éléments mis en correspondance ; il consiste en ce que les mots communs ont un nombre qui leur correspond, les autres sont décomposés en syllabes, et les plus rares analysés par lettres. Des chiffres inutiles servent à tromper les curieux.

Il faut noter que l’époque de Pascal n’avait pas encore connu le déchiffrement des hiéroglyphes égyptiens. Le jésuite Athanase Kircher s’y est attaqué, mais sans grand succès parce qu’il postulait que chaque hiéroglyphe représentait une notion abstraite. Voir Poulouin Claudine, Le temps des origines. L'Éden, le Déluge et les “temps reculés” de Pascal à l'Encyclopédie, Champion, Paris, 1998, p. 275 sq.

♦ Substitution et transposition

Le chiffre comporte deux procédés principaux, la substitution et la transposition.

La substitution consiste à remplacer, en respectant leur ordre de succession, les unités de chiffrement par des unités cryptographiques correspondantes. Voir Stern Jacques, La science du secret, p. 30. La substitution remplace chaque lettre du message par un autre symbole. Chiffre et déchiffrement passent par l’utilisation de tables de correspondance de symboles. La méthode n’offre qu’une sécurité minime. Les variantes du principe de substitution : p. 30. Il est possible d’associer à chaque lettre un choix de plusieurs symboles, appelés homophones. Voir aussi Wrixon Fred, Langages secrets, p. 178 sq. : les procédés de substitution remplacent des unités claires par des lettres, des nombres, ou des symboles tout en conservant l’ordre de succession des mots ou des lettres d’un message.

C’est apparemment le seul procédé dont Pascal tient ici compte.

Sur la transposition, voir Muller André, Les écritures secrètes, p. 7. Ce principe de chiffrement consiste à modifier l’ordre relatif des unités de chiffrement. Voir Stern Jacques, La science du secret, p. 31, et Wrixon Fred, Langages secrets, p. 144 sq. Pascal ne semble pas avoir envisagé ce second principe dans ce fragment.

De sorte qu’une langue inconnue est déchiffrable.

La langue est ainsi considérée comme un code qui peut être mis en rapport avec d’autres langues par le biais de la traduction, qui met en correspondance les mots d’une langue dans ceux d’une autre langue.

L’idée qu’une langue inconnue est déchiffrable, prend sa source dans les instructions qu’Étienne Pascal a apportées à son jeune fils. La Vie de M. Pascal de Giberte Périer en témoigne. Voir la 1^e version, § 5, OC I, éd. J. Mesnard, p. 572 : « [Étienne Pascal] lui faisait voir en général ce que c’était que les langues ; il lui montra comme on les avait réduites en grammaires sous de certaines règles ; que ces règles avaient encore des exceptions qu’on avait eu soin de remarquer : et qu’ainsi on avait trouvé moyen par là de rendre toutes les langues communicables d’un pays à l’autre ». La même indication se trouve dans la seconde version, § 4, OC I, éd. J. Mesnard, p. 604.

Force Pierre, Le problème herméneutique..., p. 122 sq., sur la cryptographie et le déchiffrement d'une langue inconnue.

Les pages de la Logique ou l’art de penser relatives aux significations accessoires montrent que les Messieurs de Port-Royal étaient conscients que, d’une langue à l’autre, les connotations attachées aux mots devaient nécessairement différer. Voir La logique ou l’art de penser, IV, ch. XV, Des idées que l’esprit ajoute à celles qui sont précisément signifiées par les mots, éd. de 1683, éd. D. Descotes, Paris, Champion, 2014, p. 681.

-------

La diversité est si ample que tous les tons de voix, tous les marchers, toussers, mouchers, éternuements [sont différents].

Sur la notion pascalienne de diversité, voir le fragment Misère 14 (Laf. 65, Sel. 99), qui use d’un effet de perspective à l’égard d’un paysage comparable à celui du présent fragment. Diversité. La théologie est une science, mais en même temps combien est-ce de sciences ? Un homme est un suppôt, mais si on l’anatomise, que sera-ce ? la tête, le cœur, l’estomac, les veines, chaque veine, chaque portion de veine, le sang, chaque humeur du sang ? Une ville, une campagne, de loin c’est une ville et une campagne, mais à mesure qu’on s’approche, ce sont des maisons, des arbres, des tuiles, des feuilles, des herbes, des fourmis, des jambes de fourmis, à l’infini. Tout cela s’enveloppe sous le nom de campagne.

Misère 9 (Laf. 60, Sel. 94). Sur quoi la fondera-t-il l’économie du monde qu’il veut gouverner ? Sera-ce sur le caprice de chaque particulier ? Quelle confusion ! Sera-ce sur la justice ? il l’ignore. Certainement s’il la connaissait il n’aurait pas établi cette maxime, la plus générale de toutes celles qui sont parmi les hommes, que chacun suive les mœurs de son pays. L’éclat de la véritable équité aurait assujetti tous les peuples. Et les législateurs n’auraient pas pris pour modèle, au lieu de cette justice constante, les fantaisies et les caprices des Perses et Allemands. On la verrait plantée par tous les états du monde, et dans tous les temps, au lieu qu’on ne voit rien de juste ou d’injuste qui ne change de qualité en changeant de climat, trois degrés d’élévation du pôle renversent toute la jurisprudence,, un méridien décide de la vérité. En peu d’années de possession les lois fondamentales changent, le droit a ses époques, l’entrée de Saturne au Lion nous marque l’origine d’un tel crime. Plaisante justice qu’une rivière borne. Vérité au deçà des Pyrénées, erreur au delà. Ils confessent que la justice n’est pas dans ces coutumes, mais qu’elle réside dans les lois naturelles communes en tout pays. Certainement ils le soutiendraient opiniâtrement si la témérité du hasard qui a semé les lois humaines en avait rencontré au moins une qui fût universelle. Mais la plaisanterie est telle que le caprice des hommes s’est si bien diversifié qu’il n’y en a point.

Contrariétés 12 (Laf. 129, Sel. 162). [Métier.] Pensées. Tout est un, tout est divers. Que de natures en celle de l’homme. Que de vacations. Et par quel hasard chacun prend d’ordinaire ce qu’il a ouï estimer. Talon bien tourné.

Louis Marin a consacré quelques études à ces fragments (voir plus bas).

On distingue des fruits les raisins, et entre ceux‑là les muscats, et puis Condrieu, et puis Desargues, et puis cette ente. Est‑ce tout ? En a‑t‑elle jamais produit deux grappes pareilles ? Et une grappe a‑t‑elle deux grains pareils ? etc.

Ente : petite portion d’un arbre qu’on fourre dans une autre par une incision qu’on y fait, afin de corriger le goût du fruit, ou même pour lui faire porter un fruit différent. On appelle aussi cela une greffe (Furetière). Le mot « ente » est utilisé en botanique ou dans le jardinage ; La manière de cultiver les arbres fruitiers de 1652, que l’on attribue à Arnauld d’Andilly, emploie constamment le verbe enter ; voir l’éd. de la Réunion des musées nationaux, Paris, 1993, p. 33. Pascal emploie le même mot dans l’expression un songe, sur lequel les autres sont entés, dans le fragment Contrariétés 14 (Laf. 131, Sel. 164). Les hésitations du copiste de C₁ sont peut-être dues au fait qu’en botanique on parle aussi de l’opération de greffe en fente, comme en témoigne aussi le livre d’Arnauld d’Andilly, éd. cit., p. 33. Voir l’étude du manuscrit et des copies.

Muscat : raisin et vin exquis qu’on met au rang des vins de liqueur, qui sent un peu le musc (Furetière). J. Douillet précise que le Condrieu n’est pas un muscat.

Mesnard Jean, “Point de vue et perspective dans les Pensées”, Courrier du Centre International Blaise Pascal, 16, p. 3 sq., repris dans Treize études sur Blaise Pascal, p. 11-24, qui suggère que le présent fragment est la description d’un tableau.

Mesnard Jean, “Desargues et Pascal”, in Desargues en son temps, in Desargues en son temps, p. 94. Illustration de l'idée de diversité. Le fragment est construit en plans successifs, le passage de l'un à l'autre s'accompagnant d'un rétrécissement du champ de vision, pour faire ressortir le divers sous l'uniforme apparent : p. 95. Toute la pensée relève d'une conception perspective arguésienne.

Marin Louis, “Une ville, une campagne, de loin... : paysages pascaliens”, Littérature, 61, fév. 1986, p. 3-16 ; repris in Pascal et Port-Royal, p. 196-213.

Marin Louis, La critique du discours. Sur la Logique de Port-Royal et les Pensées de Pascal, p. 120 sq. Prolifération à l’infini de la différence.

♦ Desargues

Sur le géomètre Girard Desargues, ami d’Étienne Pascal et du P. Mersenne, et maître de Blaise sur la géométrie ces coniques, voir Dhombres J. et J. Sakarovitch, Desargues en son temps, Blanchard, Paris, 1994.

Taton René, “Le lyonnais Girard Desargues (1591-1661) et son œuvre géométrique et technique”, in Taton René, Études d'histoire des sciences, Brepols, Turnhout, 2000, p. 69-82. Origine de la famille. Voir aussi, sur ce dernier point, Taton René, L'œuvre mathématique de Girard Desargues, p. 11 sq.

Mesnard Jean, “Desargues et Pascal”, in Desargues en son temps, p. 94. Desargues et Condrieu. Pascal a-t-il rendu visite à Desargues à Condrieu ? Il serait possible de loger un séjour de Pascal entre mai 1649 et novembre 1650 : p. 95. Il se serait alors trouvé au domaine de Château-Grillet, au-delà de Condrieu : p. 94-95.

Depuis la redécouverte de la personne et des œuvres de Desargues, dont le point de départ a été l’œuvre de Poncelet sur les Propriétés projectives des figures, de nombreuses études ont illustré son génie et l’originalité de ses inventions. Parmi les travaux les plus importants, il faut citer les ouvrages suivants ✍ :

Andersen Kirsti, The geometry of an art. The history or the mathematical theory of perspective from Alberti to Monge, New York, Springer, 2007, p. 427 sq. Ouvrage d’ensemble passionnant.

Dhombres J. et J. Sakarovitch (éd.), Desargues en son Temps, Blanchard, Paris, 1994. Recueil d’études particulièrement compréhensif.

Douillet Jacques, “Desargues, Pascal, et les raisins de Condrieu”, Écrits sur Pascal, Paris, Éd. du Luxembourg, 1959, p. 169-186.

Field Judith et Gray Jeremy, The geometrical works of Girard Desargues, Springer Verlag, New York et Berlin, 1987.

Gerhardt, “Desargues et Pascal uber die kegelshnitte”, Sitzungsberichte des Königlich preussichen Akademie der Wissenchaft zu Berlin. Sitzung des physik.-math. Classe, VIII, 1892, p. 183-204.

Granger Gilles-Gaston, Essai d’une philosophie du style, Paris, Colin, 1968.

Hilbert David, Les Fondements de la géométrie, édition critique par Paul Rossier, Dunod, Paris, 1971, rééd. Jacques Gabay, 1997. Hilbert s’appuie sur l’exemple du théorème de Desargues.

Taton René, L’œuvre mathématique de Girard Desargues, contient une bonne introduction à l’œuvre de Desargues et l’édition de son Brouillon projet d’une atteinte aux événements des rencontres d’un cône avec un plan.

L’étude de Mesnard Jean, “Desargues et Pascal”, in Desargues en son temps, p. 87-99, est la meilleure introduction à Desargues pour les pascalisants.

À l’heure actuelle, il n’existe encore qu’une édition déjà ancienne de l’œuvre de Girard Desargues, Desargues Girard, Œuvres, éd. Poudra, 2 vol., Paris, Leiber, 1864.

Abraham Bosse a été le disciple de Desargues et a contribué à répandre ses méthodes de perspective : voir Taton René, “Le lyonnais Girard Desargues (1591-1661) et son œuvre géométrique et technique”, in Taton René, Études d'histoire des sciences, Brepols, Turnhout, 2000, p. 74. Desargues confie à Bosse le soin de répandre ses méthodes, après la campagne de 1642 où il a été taxé de plagiat. Bosse s'adresse à un public moins averti que Desargues, et les tirages de ses ouvrages sont bien supérieurs à ceux de Desargues. Bosse enseigne la perspective à la manière de Desargues : p. 75.

♦ Condrieu, le village et la propriété de Desargues

Chef-lieu de canton, Condrieu est situé à la pointe sud du département du Rhône, à une quarantaine de kilomètres en aval de Lyon, au carrefour de trois provinces, le Lyonnais, le Forez et le Dauphiné. Les origines du village remontent à l’époque gallo-romaine. La batellerie a longtemps fait de Condrieu un lieu d’importance. Ses bateliers étaient réputés pour leur habileté. Les sentiers dans les coteaux (coursières) qui donnent accès aux vignes portent des noms (la Patrouilleuse, la Roncharde, Corbéry). La famille de Desargues est originaire de Condrieu. Il y possédait une vigne.

Douillet J., “Desargues, Pascal, et les raisins de Condrieu”, Écrits sur Pascal, Paris, Éd. du Luxembourg, 1959, p. 169-186. Sur la propriété de Desargues à Condrieu, Château-Grillet, voir p. 174 sq. Le Condrieu n’est pas un muscat : p. 180. Douillet pense qu’à côté du Condrieu à base de plans de vionnier, qui donnait un vin blanc de haute qualité, on cultivait quelques plans de muscat, d’une qualité inférieure : p. 180. Sur le poème d’allure galante de Dalibray sur une bouteille de Condrieu, voir p. 182.

Je n’ai jamais jugé d’une même chose exactement de même.

Mesnard Jean, Les Pensées de Pascal, 2^e éd., 1993, p. 123. ✍

Souvenir de l’opuscule De l’esprit géométrique, II, § 11, OC III, éd. J. Mesnard, p. 417. « Les principes du plaisir ne sont pas fermes et stables. Ils sont divers en tous les hommes, et variables dans chaque particulier avec une telle diversité, qu’il n’y a point d’homme plus différent d’un autre que de soi-même dans les divers temps. Un homme a d’autres plaisirs qu’une femme ; un riche et un pauvre en ont de différents ; un prince, un homme de guerre, un marchand, un bourgeois, un paysan, les vieux, les jeunes, les sains, les malades, tous varient ; les moindres accidents les changent. »

La Rochefoucauld, Maximes, n°135, éd. Truchet, Garnier, p. 36. « On est quelquefois aussi différent de soi-même que des autres. »

Je ne puis juger d’un ouvrage en le faisant. Il faut que je fasse comme les peintres et que je m’en éloigne, mais non pas trop.

Vanité 9 (Laf. 21, Sel. 55). Si on est trop jeune on ne juge pas bien, trop vieil de même. Si on n’y songe pas assez, si on y songe trop on s’entête et on s’en coiffe. Si on considère son ouvrage incontinent après l’avoir fait, on en est encore tout prévenu, si trop longtemps après, on n’y entre plus.

Ainsi les tableaux vus de trop loin et de trop près. Et il n’y a qu’un point indivisible qui soit le véritable lieu. Les autres sont trop près, trop loin, trop haut ou trop bas. La perspective l’assigne dans l’art de la peinture. Mais dans la vérité et dans la morale, qui l’assignera ?

Ce fragment peut être considéré comme la théorie dont le présent fragment est l’application.

Cette considération sur la juste distance dans la perspective rejoint le problème du point de vue fixe, auquel Michel Serres a consacré des pages importantes dans Le Système de Leibniz et ses Modèles mathématiques, t. 2, Paris, P. U. F., Paris, 1968, p. 647-712.

Mesnard Jean, Les Pensées de Pascal, 2^e éd., 1993, p. 82. ✍

Dans l’exemple du peintre, l’éloignement est d’ordre spatial. Dans celui de l’auteur, il est d’ordre chronologique.

De combien donc ? Devinez.

L’expression mais non pas trop. De combien donc ? Devinez est une addition ; la couleur de l’encre n’est pas la même. L’addition marque un retour ironique de Pascal sur son propre texte.

Le verbe deviner suppose que l’on n’a aucun élément solide pour apprécier la distance juste qu’il faut prendre.

Le défi devinez est ironique, comme en témoigne le fragment Vanité 9 (Laf. 21, Sel. 55), qui s’achève sur une interrogation similaire : Si on considère son ouvrage incontinent après l’avoir fait, on en est encore tout prévenu, si trop longtemps après, on n’y entre plus. Ainsi les tableaux vus de trop loin et de trop près. Et il n’y a qu’un point indivisible qui soit le véritable lieu. Les autres sont trop près, trop loin, trop haut ou trop bas. La perspective l’assigne dans l’art de la peinture. Mais dans la vérité et dans la morale, qui l’assignera ?

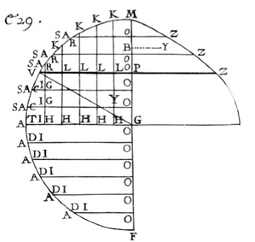
Les figures géométriques au dos du papier

La figure représente manifestement un cercle auquel est inscrit un triangle comportant un angle au centre.

Malgré l’emploi de la planche lumineuse, il est difficile de l’interpréter de manière certaine.

Si l’on admet la chronologie des papiers du manuscrit original établie par Philippe Sellier, cette figure a pu être tracée vers 1658, c’est-à-dire à l’époque où Pascal a lancé le concours sur la roulette et rédigé ses Lettres de A. Dettonville. Il peut sembler tentant de la rattacher aux derniers écrits mathématiques de Pascal. De nombreuses figures des Lettres de A. Dettonville représentent un cercle partiel ou complet avec des rayons issus d’un angle au centre. C’est notamment dans le cas des figures associées aux Traités des sinus du quart de cercle, au Traité des arcs de cercle et au Petit traité des solides circulaires.

Deux réserves préliminaires s’imposent cependant.

Primo, la photographie montre que, de l’angle de gauche du triangle, une courbe semble partir vers le haut, qui paraît être un arc de cercle, mais pourrait être un segment d’une autre courbe.

Secundo, sur aucune des figures de Dettonville n’est tracé le troisième côté du triangle, la corde de l’arc qui relie les intersections des rayons avec la circonférence, comme c’est le cas sur la figure du Recueil des originaux.

Ces réserves faites, on peut proposer une hypothèse.

Dans le Petit traité des solides circulaires, la partie préliminaire de l’Article 5, p. 3-4 de l’impression originale, OC IV, éd. J. Mesnard, p. 507-508, Pascal recherche le centre de gravité de l’arc MKV (Figure 29). Or il est bien connu que cette détermination demande, entre autres, la connaissance de la corde MV. Il est possible que la figure du manuscrit corresponde à un moment de la recherche de Pascal sur ce point. Toutefois, il ne s’agit là que d’une recherche relativement facile, qui est destinée à résoudre un problème beaucoup plus ardu, la détermination du centre de gravité de la surface courbe engendrée par la rotation de l’arc MKV autour du rayon MG. Le fait qu’il ne s’agit que d’une démonstration transitoire peut expliquer que Pascal ne lui ait pas consacré une figure particulière dans les planches déjà très chargées des Lettres de A. Dettonville, et que la figure 29 ne comporte pas de corde MV.

Selon Kokiti Hara, L’Œuvre mathématique de Pascal, p. 110, le Petit traité des solides circulaires est composé d’une collection de lemmes, comme un long scolie inséré tardivement dans l’ensemble des traités de Dettonville. Ce qui nous situe bien vers 1658-1659, puisque le volume des Lettres a été achevé début 1659 (OC IV, éd. J. Mesnard, p. 368).

Cependant, comme Pascal est loin d’avoir publié toutes ses recherches de géométrie, cette figure se rapporte peut-être à une partie inconnue de ses travaux.